|
It is sufficient to solve for s ∈ R, x ∈ R, and y ∈ R that satisfy the following equations:
One approach is to write x and y in terms of s and then solve for s using the second equation.
Example: Solve the following three problems.
-
Solve the following equation for x ∈ R:
-
Solve the following equation for x ∈ R and y ∈ R:
| |
| | and | | are linearly dependent
|
|
-
Determine if the following two vectors are linearly dependent or linearly independent:
In the case of vectors in R2, the properties of linear dependence and orthogonality can be defined in terms of
the slopes of the vectors involved. However, note that these definitions in terms of slope are a special case for R2.
The more general definitions (in terms of scalar multiplication and dot product, respectively) apply to any vectors in a vector space.
Thus, we can derive the slope definitions from the more general definitions.
Fact: If two vectors [ x; y] ∈ R2 and [ x'; y'] ∈ R2 are linearly dependent, then x/ y = x'/ y'.
If the two vectors a linearly dependent, then there exists a scalar s ∈ R such that:
Fact: If two vectors [ x; y] ∈ R2 and [ x'; y'] ∈ R2 are orthogonal, then x/ y = - y'/ x':
Example: List all unit vectors orthogonal to:
| |
It is sufficient to solve for x ∈ R and y ∈ R that satisfy the following equations:
We can solve the above for the two vectors by first solving for both possible values of
x, then finding the corresponding values for y:
Thus, the two vectors are:
Orthogonal projections of vectors have a variety of interpretations and applications; one simple interpretation of the projection of
a vector v onto a vector w is the shadow of vector v on w with respect to a light source that is orthogonal to w.
Example: Consider the vector following vectors, where u, v ∈ R2 and u is a unit vector:
What is the orthogonal projection of v onto u? It is simply the x component of v, which is x. Thus:
| | | is the projection of v onto u
|
|
Notice that we can obtain the length of the orthogonal projection using the dot product:
Since u is a unit vector, we can then simply multiply u by the scalar x to obtain the actual projection:
The above example can be generalized to an arbitrary vector v and unit vector u; then, it can be generalized to any vector u by using
the fact that u/||u|| is always a unit vector.
Example: Compute the orthogonal projection of v onto u where:
We can apply the formula:
| = | | | = | | | = | | | = | | |
(v ⋅ (u/||u||)) ⋅ (u/||u||) | |
| = | | | = | | | = | | | = | | | | = | |
Other tools available online
can be used to perform and check computations such as the above.
Example: Solve the problems below.
-
Compute the orthogonal projection of v onto u where u is a unit vector and:
We can apply the formula:
| (v ⋅ (u/||u||)) ⋅ (u/||u||) | |
| = | | | = | | | = | |
-
Compute the projection of v onto w where:
We can apply the formula:
| = | | | = | | | = | | | = | | |
(v ⋅ (w/||w||)) ⋅ (w/||w||) | |
| = | | | = | | | = | | | = | |
Fact: Given the points u = [ x1, y1] and v = [ x2, y2], we can find the equation of the line between these two points in the
form y = mx + b.
We recall the definition for a line L defined by two points:
| = | | { p | ∃ a ∈ R, p = a (u - v) + u }.
|
|
Thus, if [ x; y] is on the line, we have:
This implies the following system of equations (one from the x components in the above, and one from the y components):
If we solve for a in terms of x, we can recover a single equation for the line:
| = | | | = | | ((x - x1)/(x1 - x2)) (y1 - y2) + y1 |
| | = | | ((y1 - y2)/(x1 - x2)) (x - x1) + y1
|
|
Notice that we can set m = ( y1 - y2)/( x1 - x2) because that is exactly the slope of the line between [ x1; y1] and [ x2; y2].
We see that we can set b = - m x1 + y1.
2.5. Solving common problems involving vector algebra
We review the operations and properties of vectors introduced in this section by considering several example problems.
Example: Are the vectors [2; 1] and [3; 2] linearly independent?
There are at least two ways we can proceed in checking pairwise linear independence. Both involve checking if the vectors
are linearly dependent. If they are linearly dependent, then they cannot be linearly independent. If they are not linearly
dependent, they must be linearly independent.
We can compare the slopes; we see they are different, so they must be linearly independent.
1/2 ≠ 2/3
We can also use the definition of linear dependence. If they are linearly dependent, then we know that
Does such an a exist? We try to solve for it:
Since we derive a contradiction, there is no such a, so the two vectors are not linearly dependent, which means they
are linearly independent.
Example: Given v = [15; 20], list the vectors that are orthogonal to v, but of the same length as v.
The two constraints on the vectors [x;y] we seek are:
We take the first constraint and solve for x in terms of y.
We now plug this into the second equation.
Thus, the vectors are [-20; 15] and [20; -15].
Example: Given constants a, b, c ∈ R, find a vector orthogonal to the plane P defined
by:
| = | | { | | | a (x + y + z) + b (y + z) + c z = 0 }.
|
|
We only need to rewrite the equation defining the plane in a more familiar form. For any [ x; y; z] ∈ P, we know that:
| a (x + y + z) + b (y + z) + c z | |
| = | | |
ax + (a + b) y + (a + b + c) z | |
| = | | | = | |
In order to be orthogonal to a plane, a vector must be orthogonal to all vectors [ x; y; z] on that plane.
Since all points on the plane are orthogonal to [ a; a + b; a + b + c] by the above argument, [ a; a + b; a + b + c] is such a point.
Example: Define the line L that is orthogonal to the vector [ a; b] but also crosses [ a; b] (i.e, [ a; b] falls on the line).
We know that the line must be parallel to the vector that is orthogonal to [a; b]. The line L0 crossing [0; 0] that is orthogonal
to [a; b] is defined as:
However, we need the line to also cross the point [ a; b]. This is easily accomplished by adding the vector [ a; b] to all the points
on the orthogonal line going through [0; 0] (as defined above). Thus, we have:
If we want to find points [ x ; y ] on the line directly without the intermediate term [ x' ; y' ], we can solve for
[ x' ; y' ] in terms of [ x ; y ]:
We can then substitute to obtain a more direct definition of L (in terms of a constraint on the
vectors [ x ; y ] in L):
| = | | | = | | { ( | | − | | ) + | | | | | ⋅ ( | | − | | ) = 0 } |
| | = | |
Example: Is [7; −1] on the line defined by the points u = [19; 7] and v = [1; −5]?
To solve this problem, we recall the definition for a line defined by two points:
{ p | ∃ a ∈ R, p = a (u - v) + u }.
Thus, we want to know if [7; -1] is in the set defined as above. This can only occur if there exists
an a such that [7; -1] = a (u - v) + u.
We solve for a; if no solution exists, then the point [7; -1] is not on the line L. If an a exists, then it is. In this case,
a = 1/3 is a solution to both equations, so [7; -1] is on the line.
Example: Define the line that is orthogonal to the vector [3; 5] but also crosses [3; 5] (i.e, [3; 5] falls on the line).
We know that the line must be parallel to the vector that is orthogonal to [3; 5]. The line crossing [0; 0] that is orthogonal
to [3; 5] is defined as:
We can rewrite the above in a more familiar form:
However, we need the line to also cross the point [3; 5]. This is easily accomplished by adding the vector [3; 5] to all the points
on the orthogonal line going through [0; 0] (as defined above). Thus, we have:
We can rewrite the above by defining:
Now we substitute [ x; y] with [ x', y'] in our definition of the line:
We can now write the equation for the line:
Notice that, alternatively, we could have instead simply found the y-intercept b ∈ R of the following equation using the point [3;5]:
Example: Is [8; -6] a linear combination of the vectors [19; 7] and [1; -5]?
We recall the definition of a linear combination and instantiate it for this example:
Thus, if we can solve for a and b, then [8; −6] is indeed a linear combination.
Example: Are the vectors V = {[2; 0; 4; 0], [6; 0; 4; 3], [1; 7; 4; 3]} linearly independent?
The definition for linear independence requires that none of the vectors being considered can be expressed
as a sum of the others. Thus, we must check all pairs of vectors against the remaining third vector not in the pair.
There are 3!/(2!*1!) such pairs:
| can | | be expressed as a combination of | | and | | ? |
| |
can | | be expressed as a combination of | | and | | ? |
| |
can | | be expressed as a combination of | | and | | ?
|
|
For each combination, we can check whether the third vector is linearly dependent.
If it is linearly dependent, we can stop and say that the three vectors are not
linearly independent. If it is not, we must continue checking all the pairs. If all the pairs are incapable of
being scaled and added in some way to obtain the third vector, then the three vectors are linearly independent.
not (u, v, w are linearly independent) iff (∃ a,b ∈ R, u,v,w ∈ V, w is a linear combination of u and v)
Notice that this an example of a general logical rule:
not (∀ x ∈ S, p) iff (∃ x ∈ S, not p)
We check each possible combination and find that we derive a contradiction if we assume they are not independent.
Thus, V is a set of linearly independent vectors.
2.6. Using vectors and linear combinations to model systems
In the introduction we noted that in this course, we would define a symbolic language for working with a certain
collection of idealized mathematical objects that can be used to model system states of real-world systems in an abstract
way. Because we are considering a particular collection of objects (vectors, planes, spaces, and their relationships),
it is natural to ask what kinds of problems are well-suited for such a representation (and also what problems are
not well-suited).
What situations and associated problems can be modelled using vectors and related operators and properties?
Problems involving concrete objects that have a position, velocity, direction, geometric shape, and relationships between
these (particularly in two or three dimensions) are natural candidates. For example, we have seen that it is possible
to compute the projection of one vector onto another. However, these are just a particular example of a more general
family of problems that can be studied using vectors and their associated operations and properties.
A vector of real numbers can be used to represent an object or collection of objects with some fixed number of characteristics (each
corresponding to a dimension or component of the vector) where each characteristic has a range of possible values.
This range could be a set of magnitudes (e.g., position, cost, mass), a discrete collection of states (e.g.,
absence or presence of an edge in a graph), or even a set of relationships (e.g., for every cow, there are four
cow legs; for every $1 invested, there is a return of $0.02). Thus, vectors are well-suited for representing
problems involving many instances of objects where all the objects have the same set of possible characteristics
along the same set of linear dimensions. In these instances, many vector operations also have natural interpretations.
For example, addition and scalar multiplication (i.e., linear combinations) typically correspond to the aggregation
of a property across multiple instances or copies of objects with various properties (e.g., the total mass of a
collection of objects).
In order to illustrate how vectors and linear combinations of vectors might be used in applications, we recall the
notion of a system. A system is any physical or abstract phenomenon, or observations of a phenomenon, that
we characterize as a collection of real values along one or more dimensions. A
system state or state a system is a particular collection
of real values. For example, if a system is represented by R4, states of that system are represented by individual vectors
in R4 (note that not all vectors need to correspond to valid or possible states; see the examples below).
Example: Consider the following system: a barn with cows and chickens inside it. There are several dimensions along
which an observer might be able to measure this system (we assume that the observer has such poor eyesight that chickens and
cows are indistinguishable from above):
- number of chickens inside
- number of cows inside
- number of legs that can be seen by peeking under the door
- number of heads that can be seen by looking inside from a high window
Notice that we could represent a particular state of this system using a vector in R4. However, notice also that
many vectors in R4 will not correspond to any system that one would expect to observe. Usually, the number of
legs and heads in the entire system will be a linear combination of two vectors: the number of legs per cow,
and the number of legs per chicken:
Given this relationship, it may be possible to derive some characteristics of the system given only partial information.
Consider the following problem: how many chickens and cows are in a barn if 8 heads and 26 legs were observed?
Notice that a linear combination of vectors can be viewed as a translation from a vector describing one set of
dimensions to a vector describing another set of dimensions. Many problems might exist in which the values are
known along one set of dimensions and unknown along another set.
Example: We can restate the example from the introduction using linear combinations. Suppose we have $12,000 and two
investment opportunities: A has an annual return of 10%, and B has an annual return of 20%. How much should we invest
in each opportunity to get $1800 over one year?
The two investment opportunities are two-dimensional vectors representing the rate of return on a dollar:
The problem is to find what combination of the two opportunities would yield the desired observation of the entire system:
| | | | | 1 dollar | | 0.1 dollars of interest |
| |
|
⋅ x dollars in opportunity A
+ | | | | 1 dollar | | 0.2 dollars of interest |
| |
|
⋅ y dollars in opportunity B
| |
| = | | | | | | 12,000 dollars | | 1800 dollars of interest |
| |
|
|
|
Next, we consider a problem with discrete dimensions.
Example: Suppose there is a network of streets and intersections and the city wants to set up cameras
at some of the intersections. Cameras can only see as far as the next intersection. Suppose there are five
streets (#1, #2, #3, #4, #5) and four intersections (A, B, C, and D) at which cameras can be placed, and the city
wants to make sure a camera can see every street while not using any cameras redundantly (i.e., two cameras
should not film the same street).
Vectors in R5 can represent which streets are covered by a camera. A fixed collection of vectors, one for each
intersection, can represent what streets a camera can see from each intersection. Thus, the system's dimensions
are:
- is street #1 covered by a camera?
- is street #2 covered by a camera?
- is street #3 covered by a camera?
- is street #4 covered by a camera?
- is street #5 covered by a camera?
- is there a camera at intersection A? (represented by the variable a below)
- is there a camera at intersection B? (represented by the variable b below)
- is there a camera at intersection C? (represented by the variable c below)
- is there a camera at intersection D? (represented by the variable d below)
Four fixed vectors will be used to represent which streets are adjacent to which intersections:
Placing the cameras in the way required is possible if there is integer solution to the following equation
involving a linear combination of the above vectors:
Example: Suppose a chemist wants to model a chemical reaction. The dimensions of the system might be:
- how many molecules of C3H8 are present?
- how many molecules of O2 are present?
- how many molecules of CO2 are present?
- how many molecules of H2O are present?
- how many atoms of carbon are present?
- how many atoms of hydrogen are present?
- how many atoms of oxygen are present?
Individual vectors in R3 can be used to represent how many atoms of each element are in each type of
molecule being considered:
| C3H8: | | , O2: | | , CO2: | | , H2O: | |
|
|
Suppose we know that the number of atoms in a system may never change during a reaction, and that some quantity
of C3H8 and O2 can react to yield only CO2 and H2O. How many molecules of each compound will be involved in the reaction? That is the solution
to the following linear combination.
For example, suppose we start with 1000 molecules of C3H8 and 5000 molecules of O2. If both of these compounds react to produce only
CO2 and H2O, how many molecules of each will be produced?
Thus, a = 3000 molecules of CO2 and b = 4000 molecules of H2O will be produced.
The notion of a linear combination of vectors is common and can be used to mathematically model a wide variety of problems.
Thus, a more concise notation for linear combinations of vectors would be valuable. This is one of the issues addressed by introducing
a new type of term: the matrix.
3. Matrices
In this section we introduce a new kind of term: a matrix. We define some operations on matrices and some
properties of matrices, and we describe some of the possible ways to interpret and use matrices.
3.1. Matrices and multiplication of a vector by a matrix
Matrices are a concise way to represent and reason about linear combinations and linear independence of vectors (e.g., setwise linear
independence might be difficult to check using an exhaustive approach), reinterpretations of systems using different dimensions,
and so on. One way to interpret a matrix is as a collection of vectors. Multiplying a matrix by a vector corresponds to computing a linear
combination of that collection of vectors.
As an example, we consider the case for linear combinations of two vectors. The two scalars in the linear combination
can be interpreted as a 2-component vector. We can then put the two vectors together into a single object in our
notation, which we call a matrix.
Notice that the columns of the matrix are the vectors used in our linear combination. Notice also that we can now
reinterpret the result of multiplying a vector by a matrix as taking the dot product of each of the matrix rows with the
vector.
Fact:
| = | | | = | | | = | | | = | | | | | | (a,b) ⋅ (x,y) | | (c,d) ⋅ (x,y) |
| |
|
|
|
Because a matrix is just two column vectors, we can naturally extend this definition of multiplication
to cases in which we have multiplication of a matrix by a matrix: we simply multiply each column of the
second matrix by the first matrix and write down each of the resulting columns in the result matrix.
Definition:
| = | | | | | | (a,b) ⋅ (x,y) | (a,b) ⋅(s,t) | | (c,d) ⋅ (x,y) | (c,d) ⋅ (s,t) |
| |
|
|
|
These definitions can be extended naturally to vectors and matrices with more than two components. If we denote using Mij the entry in a matrix M found
in the ith row and jth column, then we can define the result of matrix multiplication of two matrices A and B as a matrix M such that
| Mij = ith row of A ⋅ jth column of B.
|
|
3.2. Interpreting matrices as tables of relationships and transformations of system states
We saw how vectors can be used to represent system states. We can extend this interpretation to matrices and use
matrices to represent relationships between the dimensions of system states. This allows us to interpret matrices as transformations
between system states (or partial observations of system states).
If we again consider the example system involving a barn of cows and chickens, we can reinterpret the matrix as a table of relationships between
dimensions. Each entry in the table has a unit indicating the relationship it represents.
|
chickens |
cows |
|
| heads |
1 head/chicken |
1 head/cow |
|
| legs |
2 legs/chicken |
4 legs/cow |
|
Notice that the column labels in this table represent the dimensions of an "input" vector that could be multiplied by this matrix, and
the row labels specify the dimensions of the "output" vector that is obtained as a result. That is,
if we multiply using the above matrix a vector that specifies the number of chickens and the number of cows in a system state, we will get a
vector that specifies the number of heads and legs we can observe in that system.
| | | | | 1 head/chicken | 1 head/cow | |
2 legs/chicken | 4 legs/cow |
| |
|
⋅
| |
| |
| = | |
Thus, we can interpret multiplication by this matrix as a function that takes system states that only specify the number of chickens and
cows, and converts them to system states that only specify the number of heads and legs:
(# chickens × # cows) → (# heads × # legs)
3.3. Interpreting multiplication of matrices as composition of system state transformations
Example: Suppose that we have a system with the following dimensions.
- number of wind farms
- number of coal power plants
- units of power
- units of cost (e.g., pollution)
- number of single family homes (s.f.h.'s)
- number of businesses
Two different matrices might specify the relationships between some combinations of dimensions in this system.
| M1 = | | | | 100 power/wind farm | 250 power/coal plant | |
50 cost/wind farm | 400 cost/coal plant |
| |
|
,
M2 = | | | | 4 s.f.h./unit power | -2 s.f.h./unit cost | |
1 businesses/unit power | 0 businesses/unit cost |
| |
|
|
|
Notice that these two matrices both represent transformations between partial system state descriptions.
T1: (# wind farms × # coal plants) → (units of power × units of cost)
T2: (units of power × units of cost) → (# s.f.h. × # businesses)
Notice that because the interpretion of a result obtained using the first transformation matches the interpretation of an input to the second, we
can compose these transformations to obtain a third transformation.
T2 o T1: (# wind farms × # coal plants) → (# s.f.h. × # businesses)
This corresponds to multiplying the two matrices to obtain a third matrix. Notice that the units of the resulting matrix can be computed using a
process that should be familiar to you from earlier coursework.
| | | | | 4 s.f.h./unit power | -2 s.f.h./unit cost | |
1 businesses/unit power | 0 businesses/unit cost |
| |
|
⋅
| | | | 100 power/wind farm | 250 power/coal plant | |
50 cost/wind farm | 400 cost/coal plant |
| |
|
| |
| = | |
| | | | 300 s.f.h./wind farm | 200 s.f.h./coal plant | |
100 business/wind farm | 250 businesses/coal plant |
| |
|
|
|
Thus, given some vector describing the number of wind farms and coal plants in the system, we can multiply that vector by (M2 ⋅ M1)
to compute the number of single family homes and business we expect to find in that system.
Example: Suppose that a gram of gold costs $50, while a gram of silver costs $10. After purchasing some of each, you have spent $350 on
15 grams of material. How many grams of each commodity have you purchased?
- Write down four dimensions describing this system.
-
Define a matrix A that can be used to convert a description of a system state that specifies only the amount of gold and silver purchased into
a description of the system state that specifies only the cost and total weight.
- Write down a matrix equation describing this problem and solve it to find the solution.
-
Define a matrix B such that for any description of a system state v that specifies only the total weight and amount spent, B ⋅ v
is a description of that system state that specifies the amount of gold and silver in that system state.
Example: Suppose we characterize our system in terms of two dimensions:
- number of single family homes (s.f.h.'s)
- number of power plants (p.p.'s)
In this example, instead of studying the relationships between dimensions, we want to study how the dimensions
change (possibly in an interdependent way) over time. For example, the following matrix might capture how
the system state evolves from year to year:
| M = | | | | 2 s.f.h. in year 1/s.f.h. in year 0 | -1 s.f.h. in year 1/p.p. in year 0 | |
0 p.p. in year 1/s.f.h in year 0 | 1 p.p. in year 1/p.p. in year 0 |
| |
|
|
|
We can parameterize the above in terms of a year t ∈ R. Notice that the matrix above is just a special case of the matrix below (when t = 0):
| M = | | | | 2 s.f.h. in year t+1/s.f.h. in year t | -1 s.f.h. in year t+1/p.p. in year t | |
0 p.p. in year t+1/s.f.h in year t | 1 p.p. in year t+1/p.p. in year t |
| |
|
|
|
What does M ⋅ M represent? If we consider the units, we have:
| M ⋅ M = | | | | 4 s.f.h. in year t+2/s.f.h. in year t | -3 s.f.h. in year t+2/p.p. in year t | |
0 p.p. in year t+2/s.f.h in year t | 1 p.p. in year t+2/p.p. in year t |
| |
|
|
|
Suppose v = [ x; y] ∈ R2 represents the number of single family homes and factories in a given year. We can then define the number of single
family homes and factories after t years as:
If we wanted to write the number of single family homes and factories as a function of t ∈ R and an initial state x0, y0 ∈ R, we
could nest the dot products as follows and use algebra to simplify:
| = | | 2 ( 2 ( 2 ( ... 2 (2 x0 - y0) - y0 ... ) - y0) - y0) - y0 |
| | = | | 2t x0 - (2t-1 + ... + 4 + 2 + 1) y0 |
| | = | | | = | | | = | | 0 ⋅ xt + 1 ⋅ ( ... (0 ⋅ x2 + 1 ⋅ ( 0 ⋅ x1 + (0 ⋅ x0 + 1 ⋅ y0))) ... ) |
| | = | |
3.5. Matrix operations and their interpretations
The following table summarizes the matrix operations that we are considering in this course.
| term |
definition |
restrictions |
general properties |
| M1 + M2 |
component-wise |
matrices must have
the same number of rows
and columns |
commutative,
associative,
has identity (matrix with all 0 components),
has inverse (multiply matrix by -1),
scalar multiplication is distributive
|
| M1 ⋅ M2 |
row-column-wise
dot products |
columns in M1 = rows in M2
rows in M1 ⋅ M2 = rows in M1
columns in M1 ⋅ M2 = columns in M2 |
associative,
has identity I (1s in diagonal and 0s elsewhere),
distributive over matrix addition,
not commutative in general,
no inverse in general
|
| M -1 |
|
columns in M = rows in M
matrix is invertible
|
M -1 ⋅ M = M ⋅ M -1 = I
|
The following tables list some high-level intuitions about how matrix operations can be understood.
level of
abstraction |
interpretations of multiplication
of a vector by a matrix |
| applications |
transformation of
system states |
extraction of information
about system states |
computing properties of
combinations or aggregations
of objects (or system states) |
conversion of system
state observations
from one set of dimensions
to another |
| geometry |
"moving" vectors in
a space (stretching,
skewing, rotating,
reflecting) |
projecting vectors |
taking a linear combination
of two vectors |
reinterpreting vector notation
as referring to a collection
of non-canonical vectors |
level of
abstraction |
interpretations of multiplication of two matrices |
| applications |
composition of system state
transformations or conversions |
| geometry |
sequencing of motions of vectors within
a space (stretching, skewing, rotating,
reflecting) |
level of
abstraction |
invertible matrix |
singular matrix |
| applications |
reversible transformation
of system states |
extraction of complete
information uniquely determining
a system state |
irreversible transformation
of system states |
extraction of incomplete
information about
a system state |
| geometry |
reversible transformation or motion
of vectors in a space |
projection onto a strict subset of
a set of vectors (space) |
| symbolic |
reversible transformation of
information numerically encoded in matrix
(example of such information: system of
linear equations encoded as matrix)
|
irreversible/"lossy" transformation of
information encoded in matrix |
Suppose we interpret multiplication of a vector by a matrix M as a function from vectors to vectors:
f(v) = M v.
Fact: Notice that for any M, if f(v) = M v then f is always a function because M v has only one possible result (i.e.,
matrix multiplication is deterministic) for a given M and v.
Fact: If f( v) = M v, then f is invertible if M is an invertible matrix. The inverse of f is then defined to be:
f -1(v) = M -1 v.
Notice that f -1 is a function because M -1 v only has one possible result. Notice that f -1 is the inverse of f because
f -1(f(v)) = M -1 M v = I v = v.
Fact: If the columns of a matrix M are linearly dependent and f( v) = M v, then M cannot have an inverse. We consider the case
in which M ∈ R2×2. Suppose we have that
If the columns of M are linearly dependent, then we know that there is some s ∈ R such that
This means that we can rewrite M:
Since matrix multiplication can be interpreted as taking a linear combination of the column vectors, this means that for x, y ∈ R,
But this means that for any two vectors [ x; y] and [ x'; y'], if x + sy = x' + sy' then multiplying by M will lead to the same result.
Thus, f is a function that takes two different vector arguments and maps them to the same result. If we interpret f as a relation and take
its inverse f -1, f -1 cannot be a function.
Thus, M cannot have an inverse (if it did, then f -1 would be a function).
Fact: If the columns of a matrix M are linearly independent and f( v) = M v, then M has an inverse. We consider the case
in which M ∈ R2×2. Suppose we have that
If the columns of M are linearly independent, then we know that a d - b % c ≠ 0:
Suppose we pick the following M -1:
The we have that:
| = | | | = | | (1/(a d - b c)) ⋅ | | | | a d - b c | bd - bd | | ac - ac | a d - b c |
| |
| |
| | = | | | = | |
Example: Solve the following problems.
- Determine which of the following matrices are not invertible:
The columns of the first matrix are linearly dependent, so it is not invertible. The first column of
the second matrix can be obtained by multiplying the second column by 0, so the two columns of that
matrix are linearly dependent; thus, it is not invertible. For the third matrix, the following equation
has no solution:
Thus, the third matrix is invertible. It is also possible to determine this by computing the
determinant for each matrix.
-
The matrix below is not invertible, and the following equation is true. What is the matrix? List all four of its components (real numbers).
Since the matrix is not invertible, it must be that its determinant is 0. Thus, we have the
following system of equations:
If we solve the above, we get:
3.6. Matrix properties
The following are subsets of Rn×n that are of interest in this course because they
correspond to transformations and systems that have desirable or useful properties. For some of these
sets of matrices, matrix multiplication and inversion have properties that they do not in general.
| subset of Rn×n |
definition |
closed under
matrix
multiplication |
properties of
matrix multiplication |
inversion |
| identity matrix |
∀ i,j
Mij = 1 if i=j, 0 otherwise |
closed |
commutative,
associative,
distributive with addition,
has identity |
has inverse (itself);
closed under inversion |
| elementary matrix |
can be obtained via an
elementary row operation
from I:
- add nonzero multiple
of one row of the matrix
to another row
- multiply a row by a
nonzero scalar
- swap two rows of the
matrix
Note: the third is a combination
of the first two operations.
|
|
associative,
distributive with addition,
have identity |
have inverses;
closed under inversion |
| scalar matrices |
∃ s ∈ R, ∀ i,j
Mij = s if i=j, 0 otherwise |
closed |
commutative,
associative,
distributive with addition,
have identity |
nonzero members
have inverses;
closed under inversion |
| diagonal matrices |
∀ i,j
Mij ∈ R if i=j, 0 otherwise |
closed |
associative,
distributive with addition,
have identity |
nonzero members
have inverses;
closed under inversion |
matrices with
constant diagonal |
∀ i,j
Mii = Mjj |
|
associative,
distributive with addition,
have identity |
|
| symmetric matrices |
∀ i,j
Mij = Mji |
|
associative,
distributive with addition,
have identity |
|
symmetric matrices
with constant diagonal |
∀ i,j
Mii = Mjj and Mij = Mji |
closed |
commutative,
associative,
distributive with addition,
have identity |
|
| upper triangular matrices |
∀ i,j
Mij = 0 if i > j |
closed |
associative,
distributive with addition,
have identity |
not invertible in general;
closed under inversion
when invertible |
| lower triangular matrices |
∀ i,j
Mij = 0 if i < j |
closed |
associative,
distributive with addition,
have identity |
not invertible in general;
closed under inversion
when invertible |
| invertible matrices |
∃ M -1 s.t. M -1 M = M M -1 = I |
closed |
associative,
distributive with addition,
have identity |
nonzero members
have inverses;
closed under inversion |
| square matrices |
all of Rn×n |
closed |
associative,
distributive with addition,
have identity |
|
Two facts presented in the above table are worth noting.
Fact: Suppose A is invertible. Then the inverse of A -1 is A, because A A -1 = I. Thus, (A -1) -1 = A.
Fact: If A and B are invertible, so is AB. That is, invertible matrices are closed under matrix multiplication. We can show
this by using the associativity of matrix multiplication. Since A and B are invertible, there exist B -1 and A -1 such that:
Thus, since there exists a matrix (B -1 A -1) such that (B -1 A -1) A B = I, (B -1 A -1) is the inverse of AB.
Example:
Given an invertible upper triangular matrix M ∈ R2×2,
show that M -1 is also upper triangular. Hint: write out
the matrix M explicitly.
Suppose we have the following upper triangular matrix:
If it is invertible, then there exists an inverse such that:
This implies that
Because M is invertible, we know that z ≠ 0. Since zc = 0, This means that c = 0. Thus, we have that the inverse is upper triangular.
Alternatively, we can observe that c = 0, and that using the formula for the inverse would yield a lower-left
matrix entry equal to −c/(det M) = 0.
Example: In terms of a, b ∈ R where a ≠ 0 and b ≠ 0, compute the inverse of:
| | | | | | | |
While we could perform the instances of matrix multiplication step-by-step and then invert the result (either by solving an equation or
using the formula for the inverse of a matrix in R2×2), it's easier to recall that diagonal matrices behave in a manner that is very
similar to the real numbers. Thus, the above product is equal to
| | ,
and its inverse simply has the multiplicative inverses of the two diagonal entries as its diagonal entries:
| | .
Another fact not in the table is also worth noting.
Fact: Any product of a finite number of elementary row matrices is invertible. This fact follows from the fact that all
elementary matrices are invertible, and that the set of invertible matrices is closed under multiplication.
Given the last fact, we might ask whether the opposite is true: are all invertible matrices the product of a finite number of elementary
matrices? The answer is yes, as we will see further below.
3.7. Solving the equation M v = w for M with various properties
Recall that for v,w ∈ Rn and M ∈ Rn×n, an equation of the following form
can represent a system of equations:
M v = w
Notice that if M is invertible, we can solve for v by multiplying both sides by M -1. More generally, if M is a member of
some of the sets in the above table, we can find straightforward algorithms for solving such an equation for v.
| M is ... |
algorithm to solve M v = w for v |
| the identity matrix |
w is the solution |
| an elementary matrix |
perform a row operation on M to obtain I;
perform the same operation on w |
| a scalar matrix |
divide the components of w by the scalar |
| a diagonal matrix |
divide each component of w by the
corresponding matrix component |
| an upper triangular matrix |
start with the last entry in v, which is easily obtained;
move backwards through v, filling in the values by
substituting the already known variables
|
| a lower triangular matrix |
start with the first entry in v, which is easily obtained;
move forward through v, filling in the values by
substituting the already known variables
|
product of a lower triangular matrix
and an upper triangular matrix |
combine the algorithms for upper and lower triangular
matrices in sequence (see example below)
|
| an invertible matrix |
compute the inverse and multiply w by it |
Example: We consider an equation M v = w where M is a diagonal matrix (the identity matrix and all scalar matrices are also diagonal
matrices).
Example: We consider an equation M v = w where M is a lower triangular matrix.
Fact: Suppose that M = L U where L is lower triangular and U is upper triangular. How can we solve M v = w?
First, note that because matrix multiplication is associative, we have
We introduce a new vector for the intermediate result U v, which we call u. Now, we have a system of matrix equations.
We first solve for u using the algorithm for lower triangular matrices, then we solve for v using the algorithm for upper triangular
matrices.
Example: Solve the following equation for x, y, z ∈ R:
We first divide the problem into two steps using the intermediate vector [ a ; b ; c ]:
Example: The inverse of a matrix in R2×2 can be computed as follows.
| = | | | | | | d/(ad − bc) | −b/(ad-bc) | | −c/(ad − bc) | a/(ad − bc) |
| |
|
|
|
Thus, if we find that the determinant of a matrix M ∈ R2×2 is nonzero, the algorithm for solving M v = w is
straightforward. Consider the following example.
| = | | | = | | | = | |
| | | | 4/((1⋅4)-(2⋅3)) | −2/((1⋅4)-(2⋅3)) | | −3/((1⋅4)-(2⋅3)) | 1/((1⋅4)-(2⋅3)) |
| |
| | | |
| | = | | | = | |
3.8. Row echelon form and reduced row echelon form
We define two more properties that a matrix may possess.
| M is in row echelon form |
- all nonzero rows are above any rows consisting of all zeroes
- the first nonzero entry (from the left) of a nonzero row is strictly
to the right of the first nonzero entry of the row above it
- all entries in a column below the first nonzero entry in a row are zero
(the first two conditions imply this)
|
| M is in reduced row echelon form |
- M is in row echelon form
- the first nonzero entry in every row is 1;
this 1 entry is the only nonzero entry in its column
|
We can obtain the reduced row echelon form of a matrix using a sequence of appropriately chosen elementary row operations.
Example: Suppose we want to find the reduced row echelon form of the matrix below. We list the steps of the procedure.
Fact: For any matrix M, there may be more than one way to reach the reduced row echelon form using elementary row operations. However,
it is always possible, and there is exactly one unique reduced row echelon form for that matrix M. We do not prove this result in this course,
but fairly short proofs by induction can be found elsewhere (such as here).
Because the reduced row echelon form of a matrix M is unique, we use the following notation to denote it:
rref M.
Example: Determine which of the following matrices are elementary:
The matrices are:
(a) not elementary (not square, so not invertible),
(b) not elementary (composition of two elementary row operations applied to the identity),
(c) not elementary (multiplication of a row by the 0 scalar is not invertible),
and (d) elementary (multiple of first row added to last row).
Example: Determine which of the following matrices are in reduced row echelon form:
The matrices are:
(a) in reduced row echelon form,
(b) not in reduced row echelon form,
(c) in reduced row echelon form,
(d) not in reduced row echelon form,
and (e) in reduced row echelon form.
Example: Suppose the matrix below is in reduced row echelon form. Solve for a, b ∈ R.
Without loss of generality, we can focus on four possibility: a is either zero or nonzero, and
b is either zero or nonzero. We can further simplify this by considering 1 as the only nonzero
value of interest. Then we have that:
- if a = 0 and b = 0, then the matrix is not in reduced row echelon form;
- if a = 0 and b = 1, then the matrix is not in reduced row echelon form;
- if a = 1 and b = 0, then the matrix is in reduced row echelon form;
- if a = 1 and b = 1, then the matrix is not in reduced row echelon form.
Thus, a = 1 and b = 0.
Question: For a given matrix in reduced row echelon form, how many different matrices can be reduced to it (one or more than one)?
Fact: It is always true that rref M = rref (rref M). Thus, the rref operation is idempotent.
Fact: If rref M is I (the identity matrix), then M is invertible. This is because I is an elementary matrix, and the row operations
used to obtain rref M from M can be represented as a product of elementary (and thus, invertible) matrices E1 ⋅ ... ⋅ En. Thus, we have:
| = | | |
(E -1n ⋅ ... ⋅ E -11) ⋅ E1 ⋅ ... ⋅ En ⋅ M | |
| = | | (E -1n ⋅ ... ⋅ E -11) ⋅ I |
| | = | | (E -1n ⋅ ... ⋅ E -11) ⋅ I
|
|
Since elementary matrices and I are invertible, and invertible matrices are closed under matrix multiplication, M must be invertible, too.
Fact: A matrix M ∈ Rn×n is not invertible iff the bottom row of rref M has all zeroes. This is because when all
rows of rref M ∈ Rn×n have at least one nonzero value, rref M must be the identity matrix (try putting a nonzero value on the bottom row, and see what the
definition of reduced row echelon form implies about the rest of the matrix). Since rref M = I, this implies that M must then be invertible by the fact immediately above this one.
Fact: For any invertible matrix M ∈ Rn×n, the reduced row echelon form of M is I ∈ Rn×n.
We can show this is true using a proof by contradiction. Suppose that M is invertible, but rref M ≠ I. We know that rref M can be
obtained via a finite number of elementary row operations E1 ⋅ ... ⋅ En:
(E1 ⋅ ... ⋅ En) M = rref M.
If rref M is not I, then the last row of rref M must consist of only zeroes. But because M is invertible, we have:
Since the product of elementary matrices is invertible, (rref M) ⋅ M -1 is also invertible. But if the last row of rref M consists of only
zeroes, then the last row of (rref M) M -1 also contains only zeroes, so it cannot be that (rref M) M -1 is invertible. Thus, we have a contradiction, so our assumption that rref M ≠ I is false.
The following table provides an alternative illustration of how the contradiction is derived:
| M is invertible |
rref M ≠ I |
| the matrix M -1 exists |
the last row of rref M is all zeroes |
| (E1 ⋅ ... ⋅ En) M = rref M |
| ((E1 ⋅ ... ⋅ En) M) M -1 = (rref M) ⋅ M -1 |
| E1 ⋅ ... ⋅ En = (rref M) ⋅ M -1 |
the last row of (rref M) ⋅ M -1
is all zeroes |
(rref M) ⋅ M -1 is invertible
because it is a product of the
invertible matrices E1, ..., En |
(rref M) ⋅ M -1 is not invertible
because multiplication by it is
a many-to-one function |
The above result implies the following fact.
Fact: If a matrix M is invertible, it is the product of a finite number of elementary matrices. This is because rref M is
the identity, which is an elementary matrix, and M can be reduced via a finite number of invertible row operations to I. Thus, the
elementary matrices can be used to generate every possible invertible matrix.
Example: Suppose that for some matrix M ∈ R2×2, the following row operations can be applied to M (in the order
specified) to obtain the identity matrix I:
- add the bottom row to the top row;
- swap the two rows;
- multiply the bottom row by 1/3.
Find the matrix M -1.
We know that performing the three row operations on M will result in I. Thus,
we can write out the row operations as three matrices E1, E2, and E3:
Thus, we have that:
We can also find M:
The following table summarizes the results.
| fact |
justification |
| (1) |
{M | M is a finite product of elementary matrices} |
= |
{M | rref M = I} |
I is an elementary matrix;
sequences of row operations
are equivalent to multiplication by
elementary matrices |
| (2) |
{M | M is a finite product of elementary matrices} |
⊂ |
{M | M is invertible} |
elementary matrices are invertible;
products of invertible matrices are invertible |
| (3) |
{M | rref M = I} |
⊂ |
{M | M is invertible} |
fact (1) in this table;
fact (2) in this table;
transitivity of equality |
| (4) |
{M | M is invertible} |
⊂ |
{M | rref M = I} |
proof by contradiction;
non-invertible M implies
rref M has all zeroes in bottom row |
| (5) |
{M | M is invertible} |
= |
{M | rref M = I} |
for any sets A,B,
A ⊂ B and B ⊂ A
implies A = B |
| (6) |
{M | M is a finite product of elementary matrices} |
= |
{M | M is invertible} |
fact (1) in this table;
fact (5) in this table;
transitivity of equality |
Given all these results, we can say that the properties for a matrix M in the following table are all equivalent:
if any of these is true, then all of them are true. If any of these is false, then all of them are false.
| M is invertible |
| det M ≠ 0 |
| the columns of M are (setwise) linearly independent |
| Mv = w has exactly one solution |
| M is a finite product of elementary matrices |
Fact: For matrices M ∈ Rn×n, rref M is guaranteed to be upper triangular. Notice that this means that for some finite
product of elementary matrices E1 ⋅ ... ⋅ En, it is the case that
M = (E1 ⋅ ... ⋅ En) ⋅ U.
If E1 ,..., En are all lower triangular, then then M has an LU decomposition. However, this will not always be the case. But recall that
E1 ,..., En are all elementary matrices.
Fact: Given any product of elementary matrices E1 ⋅ ... ⋅ En, it is possible to find a lower triangular matrix
L by applying a finite number of elementary swap operations
S1 ,..., Sn such that L = S1 ⋅ ... ⋅ Sn ⋅ E1 ⋅ ... ⋅ En is lower triangular; then we have:
| = | | S1 ⋅ ... ⋅ Sn ⋅ E1 ⋅ ... ⋅ En |
| |
(Sn -1 ⋅ ... ⋅ S1 -1) ⋅ L | |
| = | |
Thus, E1 ⋅ ... ⋅ En can be decomposed into a lower triangular matrix and a product of elementary swap matrices.
Fact: Any product of a finite number of swap elementary matrices S1 ,..., Sn is a permutation matrix.
Fact: Any matrix M can be written as the product of three matrices P ⋅ L ⋅ U where P is a permutation matrix, L is a lower-triangular matrix, and U is an upper-triangular matrix,
where:
Example: Suppose we have a system in which a single object is traveling along one spatial dimension (i.e., in a straight line).
The object has a distance travelled, a velocity, and an acceleration; these are the three dimensions of the system:
- distance (m)
- velocity (m/s)
- acceleration (m/s2)
Consider the following equations that can be used to compute the distance the object travels and its final velocity given its
acceleration a ∈ R+, initial velocity v0 ∈ R+, and the amount of time t ∈ ∈ R+ it travels.
Suppose we want to convert a view of the system state that describes the acceleration and velocity at time 0 into a view of the system
state that represents the distance travelled and velocity at time t. This conversion operation can be represented using a matrix M.
| = | | | | | | 0.5 t2 dist. at t+1 / accel. at t | t dist. at t+1 / vel. at t | |
t vel. at t+1 / accel. at t | 1 vel. at t+1 / vel. at t |
| |
| |
| | = | | | | | | 0.5 t2 m / (m/s2) | t m / (m/s) | |
t (m/s) /(m/s2) | 1 (m/s)/(m/s) |
| |
| |
| | = | | | | | | 0.5 t2 s2 | t s | |
t s | 1 scalar identity |
| |
|
|
|
This matrix is invertible. This immediately tells us that it is possible to derive the initial
acceleration and velocity given only the amount of time that has elapsed,
the distance travelled, and the final velocity.
By computing the inverse of this matrix, we can obtain formulas that allow us to derive the
initial velocity and acceleration of an object given how much time has passed, how far it has travelled, and its current velocity.
| = | |
| | | | -2/t2 accel. at t / dist. at t+1
| t accel. at t / vel. at t+1
| | t vel. at t / dist. at t+1
| 1 vel. at t / vel. at t+1
|
| |
| |
| | = | |
| | | | -2/t2 (m/s2)/m
| 2/t (m/s2) / (m/s)
| | 2/t (m/s) / m
| -1 (m/s)/(m/s)
|
| |
| |
| | = | |
| | | | -2/t2 1/s2
| 2/t 1 / s
| | 2/t 1 / s
| -1 scalar identity
|
| |
|
|
|
The formulas can be obtained by multiplying M -1 by a system state describing the distance travelled and current velocity.
This yields:
We could have also obtained the above formulas using manipulation of equations of real numbers,
or via the corresponding row operations. Let us consider the latter approach:
| = | | |
| | | | 0.5 t2 | t | | t − (2/t ⋅ 0.5 t2) | 1 − (2/t ⋅ t) |
| |
| ⋅ | | | |
| = | | | = | | | = | | |
| | | | 0.5 t2 − (t ⋅ 0) | t − (t ⋅ 1) | | 0 | 1 |
| |
| ⋅ | | | |
| = | | | | | | d − (t ⋅ ((2d/t) − v)) | | (2d/t) − v |
| |
| |
| | = | | | = | | | | | | (2/t2) ⋅ (− d + v t) | | (2d / t) − v |
| |
| |
| | = | |
3.9. Matrix transpose
Definition: The transpose of a matrix M ∈ Rn×n, denoted M⊤, is defined to be A such that for all i and j, Aij = Mji.
Fact: If a matrix M is scalar, diagonal, or symmetric, M⊤ = M. If a matrix M is upper triangular, M⊤ is lower triangular (and vice versa).
Example: Below are some examples of matrices and their transposes:
Fact: For A, B ∈ Rn×n, it is always the case that:
Fact: It is always the case that ( AB) ⊤ = B⊤ A⊤. If M = AB, then:
| = | | ith row of A ⋅ jth column of B |
| | = | | ith column of A⊤ ⋅ jth row of B⊤ |
| | = | | jth row of B⊤ ⋅ ith column of A⊤ |
| | = | |
Example: We consider the following example with matrices in R3× 3. Let a, b, c, x, y, and z be vectors in R3, with
vi representing the ith entry in a vector v. Suppose we have the following product of two matrices. Notice that a, b, and c are the rows of the left-hand matrix,
and x, y, and z are the columns of the right-hand matrix.
| | | | | a1 | a2 | a3 | | b1 | b2 | b3 | | c1 | c2 | c3 |
| |
|
⋅
| | | | x1 | y1 | z1 | | x2 | y2 | z2 | | x3 | y3 | z3 |
| |
|
| |
| = | |
| | | | (a1, a2, a3) ⋅ (x1, x2, x3) | (a1, a2, a3) ⋅ (y1, y2, y3) | (a1, a2, a3) ⋅ (z1, z2, z3)
| | (b1, b2, b3) ⋅ (x1, x2, x3) | (b1, b2, b3) ⋅ (y1, y2, y3) | (b1, b2, b3) ⋅ (z1, z2, z3)
| | (c1, c2, c3) ⋅ (x1, x2, x3) | (c1, c2, c3) ⋅ (y1, y2, y3) | (c1, c2, c3) ⋅ (z1, z2, z3)
|
| |
| |
| | = | | | | | | a ⋅ x | a ⋅ y | a ⋅ z
| | b ⋅ x | b ⋅ y | b ⋅ z
| | c ⋅ x | c ⋅ y | c ⋅ z
|
| |
|
|
|
Suppose we take the transpose of both sides of the equation above. Then we would have:
|
( | | | | a1 | a2 | a3 | | b1 | b2 | b3 | | c1 | c2 | c3 |
| |
|
⋅
| | | | x1 | y1 | z1 | | x2 | y2 | z2 | | x3 | y3 | z3 |
| |
| )⊤
| |
| = | |
| | | | a ⋅ x | a ⋅ y | a ⋅ z
| | b ⋅ x | b ⋅ y | b ⋅ z
| | c ⋅ x | c ⋅ y | c ⋅ z
|
| |
| ⊤ |
| | = | | | | | | a ⋅ x | b ⋅ x | c ⋅ x
| | a ⋅ y | b ⋅ y | c ⋅ y
| | a ⋅ z | b ⋅ z | c ⋅ z
|
| |
| |
| | = | |
| | | | x ⋅ a | x ⋅ b | x ⋅ c
| | y ⋅ a | y ⋅ b | y ⋅ c
| | z ⋅ a | z ⋅ b | z ⋅ c
|
| |
| |
| | = | |
| | | | x1 | x2 | x3
| | y1 | y2 | y3
| | z1 | z2 | z3 |
| |
|
⋅
| | | | a1 | b1 | c1
| | a2 | b2 | c2
| | a3 | b3 | c3 |
| |
| |
| | = | |
| | | | x1 | y1 | z1 | | x2 | y2 | z2 | | x3 | y3 | z3 |
| |
| ⊤
⋅
| | | | a1 | a2 | a3 | | b1 | b2 | b3 | | c1 | c2 | c3 |
| |
| ⊤
|
|
Fact: If A is invertible, then so is A⊤. This can be proven using the fact directly above.
\forall A,B \in \R^(2 \times 2),
`(A) is invertible`
\implies
(A^(-1)) * A = [1 , 0; 0 , 1]
A^\t * (A^(-1))^\t = ((A^(-1)) * A)^\t
`` = [1,0;0,1]^\t
`` = [1,0;0,1]
Fact: det A = det A⊤. We can see this easily in the A ∈ R2×2 case.
\forall a,b,c,d \in \R,
\det [a,b;c,d] = a d-b c
`` = a d - c b
`` = \det [a,c;b,d]
\det [a,b;c,d] = \det [a,c;b,d]
3.10. Orthogonal matrices
Definition: A matrix M ∈ Rn×n is orthogonal iff M⊤ = M -1.
Fact: The columns of orthogonal matrices are always orthogonal unit vectors.
The rows of orthogonal matrices are always orthogonal unit vectors.
We can see this in the R2×2 case. For columns, we use the fact that
M⊤ ⋅ M = I:
| = | | | = | | |
| | | | (a,c) ⋅ (a,c) | (a,c) ⋅ (b,d) | | (b,d) ⋅ (a,c) | (b,d) ⋅ (b,d) |
| |
| | |
| = | |
For rows, we use that M ⋅ M⊤ = I:
| = | | | = | | |
| | | | (a,b) ⋅ (a,b) | (a,b) ⋅ (c,d) | | (c,d) ⋅ (a,b) | (c,d) ⋅ (c,d) |
| |
| | |
| = | |
Below, we provide a verifiable argument of the above fact for the R2×2 case.
\forall a,b,c,d \in \R,
[a,b;c,d] * [a,b;c,d]^\t = [1,0;0,1]
\implies
[a,b;c,d] * [a,c;b,d] = [1,0;0,1]
[a a + b b, a c + b d; c a + d b, c c + d d] = [1,0;0,1]
a a + b b = 1
[a;b] * [a;b] = 1
||[a;b]|| = 1
`([a;b]) is a unit vector`
c c + d d = 1
[c;d] * [c;d] = 1
||[c;d]|| = 1
`([c;d]) is a unit vector`
a c + b d = 0
[a;b] * [c;d] = 0
`([a;b]) and ([c;d]) are orthogonal`
Fact: Matrices representing rotations and reflections are orthogonal. We can show this for the general (counterclockwise) rotation matrix:
| = | | | = | | | | | | cos 2 θ + sin 2 θ | -cos θ sin θ + sin θ cos θ | | -sin θ cos θ + cos θ sin θ | sin 2 θ + cos 2 θ |
| |
| |
| | = | |
Example: Suppose that the hour hand of an animated
12-hour clock face is represented using a vector [ x ; y ]. To
maintain the time, the coordinates [ x ; y ] must be updated once
every hour by applying a matrix M to the vector representing
the hour hand. What is the matrix M?
Since the hour hand must be rotated by 360/12 = 30 degrees in the clockwise direction while
the rotation matrix represents counterclockwise rotation, we actually want to find the
rotation matrix for 360 - (360/12) = 330 degrees.
Thus, M must be the rotation matrix for θ = 2π - (2π / 30), where θ is specified
in radians. Thus, we have:
| = | | | = | | | = | | | | | | cos (330/360 ⋅ 2π) | −sin (330/360 ⋅ 2π) | | sin (330/360 ⋅ 2π) | cos (330/360 ⋅ 2π) |
| |
| |
| | = | |
Example: You are instructed to provide a simple algorithm for
drawing a spiral on the Cartesian plane. The spiral is obtained using
counterclockwise rotation, and for every 360 degree
turn of the spiral, the spiral arm's distance from the origin
should double. Provide a matrix M ∈ R2×2 that will
take any point [ x ; y ] on the spiral and provide the next point
[ x' ; y' ] after θ radians of rotation (your definition of
M should contain θ).
It is sufficient to multiply a rotation matrix by a scalar
matrix that scales a vector according to the angle of
rotation. If the angle of rotation is θ, then the
scale factor s should be such that:
In the above, if n = π/θ then s is the nth root of 2.
Thus M would be:
| = | | | | | | 2θ/(2π) cos θ
| − (2θ/(2π)) sin θ
| | 2θ/(2π) sin θ
| 2θ/(2π) cos θ |
| |
| |
| |
Fact: Orthogonal matrices are closed under multiplication. For orthogonal A, B ∈ Rn×n we have:
Fact: Orthogonal matrices are closed under inversion and transposition. For orthogonal A ∈ Rn×n we have:
Thus, we can show that both A -1 and A⊤ are orthogonal.
We can summarize this by adding another row to our table of matrix subsets.
| subset of Rn×n |
definition |
closed under
matrix
multiplication |
properties of
matrix multiplication |
inversion |
| orthogonal matrices |
M⊤ = M -1 |
closed |
associative,
distributive with addition,
have identity |
nonzero members
have inverses;
closed under inversion |
Example: Let A ∈ R2×2 be an orthogonal matrix. Compute A A⊤ A.
We recall that because A is orthogonal, A⊤ = A -1. Thus, we have that
A A⊤ A = (A A -1) A = I A = A.
Fact: Suppose the last row of a matrix M ∈ Rn×n consists of all zeroes. Show that M is not invertible.
Suppose M is invertible. Then M⊤ is invertible. But the last column of M is all zeroes, which means it is a trivial linear
combination of the other column vectors of M. Thus, we have a contradiction, so M cannot be invertible.
3.11. Matrix rank
Yet another way to characterize matrices is by considering their rank.
Definition: We can define a the rank of a matrix M, rank M, as the number of nonzero rows in rref M.
We will see in this course that rank M is related in many ways to the various characteristics of a matrix.
Fact: Matrix rank is preserved by elementary row operations. Why is this the case? Because rref is idempotent and rank is defined in
terms of it:
| = | | |
number of nonzero rows in rref M | |
| = | | number of nonzero rows in rref (rref M) |
| | = | |
Fact: If M ∈ Rn×n is invertible, rank M = n. How can we prove this? Because all invertible matrices
have rref M = I, and I has no rows with all zeroes. If I ∈ Rn×n, then I has n nonzero rows.
Fact: For A ∈ Rn×n, rank A = rank (A⊤).
We will not prove the above in this course in general, but typical proofs
involve first proving that for all A ∈ Rn×n, rank A ≤ rank (A⊤). Why is this sufficient to complete the proof? Because we
can apply this fact for both A and A⊤ and use the fact that (A⊤)⊤ = A:
To get some intuition about the previous fact, we might consider the following question: if the columns of a matrix M ∈ R2×2
are linearly independent, are the rows also linearly independent?
Fact: The only matrix in Rn×n that has no nonzero rows in reduced row echelon form is I.
Fact: If a matrix M ∈ Rn×n has rank n, then it must be that rref M = I (and, thus, M is invertible). This is derived from
the fact above.
Fact: Invertible matrices are closed under the transposition operation. In other words, if M is invertible, then M⊤ is invertible. How
can we prove this using the rank operator? We know that rank is preserved under transposition, so we have:
Thus, the rank of rank(A⊤) is n, so it is invertible.
The following table summarizes the important facts about the rank and rref operators.
| rank (rref M) = rank M |
| rref (rref M ) = rref M |
| rank (M⊤) = rank M |
| for M ∈ Rn×n, M is invertible iff rank M = n |
Review 1. Vector and Matrix Algebra and Applications
The following is a breakdown of what you should be able to do at this point in the course
(and of what you may be tested on in an exam).
Notice that many of the tasks below can be composed.
This also means that many problems can be solved in more than one way.
- vectors
- definitions and algebraic properties of scalar and vector operations (addition, multiplication, etc.)
- vector properties and relationships between vectors
- dot product of two vectors
- norm of a vector
- unit vectors
- orthogonal projection of a vector onto another vector
- orthogonal vectors
- linear dependence of two vectors
- linear independence of two vectors
- linear combinations of vectors
- linear independence of three vectors
- lines and planes
- line defined by a vector and the origin ([0; 0])
- line defined by two vectors
- line in R2 defined by a vector orthogonal to that line
- plane in R3 defined by a vector orthogonal to that plane
- matrices
- algebraic properties of scalar and matrix multiplication and matrix addition
- collections of matrices and their properties (e.g., invertibility, closure)
- identity matrix
- elementary matrices
- scalar matrices
- diagonal matrices
- upper and lower triangular matrices
- matrices in reduced row echcelon form
- determinant of a matrix in R2×2
- inverse of a matrix and invertible matrices
- other matrix operations and properties
- determine whether a matrix is invertible
- using the determinant for matrices in R2×2
- using facts about rref for matrices in Rn×n
- algebraic properties of matrix inverses with respect to matrix multiplication
- transpose of a matrix
- algebraic properties of transposed matrices with respect to matrix addition, multiplication, and inversion
- matrix rank
- matrices in applications
- solve an equation of the form LU = w
- matrices and systems of states
- interpret partial observations of system states as vectors
- interpret relationships betweem dimensions in a system of states as a matrix
- given a partial description of a system state and a matrix of relationships, find the full description of the system state
- interpret system state transitions/transformations over time as matrices
- population growth/distributions over time
- compute the system state after a specifieds amount of time
- find the fixed point of a transition matrix
Below is a comprehensive collection of review problems going over the course material covered until this point. These problems are an
accurate representation of the kinds of problems you may see on an exam.
Example: Find any h ∈ R such that the following two vectors are linearly independent.
There are many ways to solve this problem. One way is to use the definition of linear dependence and find an h that does not satisfy it.
Then, we have that any h such that h ≠ -8 is sufficient to contradict linear dependence (and, thus, imply linear independence):
Another solution is to recall that orthogonality implies linear independence. Thus, it is sufficient to find h such that
the two vectors are orthogonal.
This implies h = 100.
| 5(20) + (-5)(-20) + (-2)h | |
| = | | | = | |
Example: Suppose we have a matrix M such that the following three equations are true:
Compute the following:
We should recall that multiplying a matrix by a canonical unit vector with 1 in the ith row in the vector gives us the ith column of the matrix.
Thus, we can immediately infer that:
Thus, we have:
| = | | | | | | (3,3,-3) ⋅ (2,1,-1) | | (-2,0,1) ⋅ (2,1,-1) |
| |
| | |
| = | |
Example: List at least three properties of the following matrix:
| |
The matrix has many properties, such as:
- it is an elementary matrix
- it is an invertible matrix
- it is an orthogonal matrix
- it is a symmetric matrix
- it has rank n
- its reduced row echelon form is the identity
Example: Find the matrix B ∈ R2×2 that is symmetric, has a constant diagonal
(i.e., all entries on the diagonal are the same real number), and satisfies the following
equation:
We know that B is symmetric and has a constant diagonal, so we need to solve for a and b in:
Example: Compute the inverse of the following matrix:
| |
One approach is to set up the following equation and solve for a,b,c, and d:
Another approach is to apply the formula for the inverse of a matrix in R2×2:
Example: Let a ∈ R be such that a ≠ 0. Compute the inverse of the following matrix:
| |
As in the previous problem, we can either solve an equation or apply the formula:
Example: Suppose x ∈ R is such that x ≠ 0. Compute the inverse of the following matrix:
| |
Because we have an upper triangular matrix, computing the inverse by solving the following equation is fairly efficient. Start by considering
the bottom row and its product with each of the columns. This will generate the values for g, h, and i. You can then proceed to the other
rows.
The solution is:
| | | | 1/x | 0 | 1/(2x) | | 0 | 1/x | 0 | | 0 | 0 | 1/4x |
| |
|
Example: Assume a matrix M ∈ R2×2 is symmetric, has constant diagonal, and all its entries are nonzero. Show that A cannot
be an orthogonal matrix.
Let a ≠ 0 and b ≠ 0, and let us define:
Suppose that M is an orthogonal matrix; then, we have that:
Thus, we have ba + ab = 0, so 2ab = 0. This implies that either a = 0 or b = 0. But this contradicts the assumptions, so M cannot be
orthogonal.
Example: Suppose the Earth is located at the origin and your spaceship is in space at the location corresponding to the vector
[ -5 ; 4; 2 ]. Earth is sending transmissions along the vector [ √(3)/3 ; √(3)/3 ; √(3)/3 ]. What is the shortest distance
your spaceship must travel in order to hear a transmission from Earth?
By the triangle inequality, for any vector v ∈ R3, the closest point to v on a line is the orthogonal projection
of v onto that line. We need to find the distance from the spaceship's current position to that point.
We first compute the orthogonal projection of [ -5 ; 4; 2 ] onto the line L
defined as follows:
We can compute the orthogonal projection using the formula for an orthogonal projection of one vector onto another.
Notice that the vector specifying the direction of transmission is already a unit vector:
Now, we must compute the distance between the destination above and the spaceship's current position:
| = | | | = | | √((16/3)2 + (-11/3)2 + (-5/3)2) |
| | = | | | = | |
Thus, the shortest distance is √(402)/3.
Example: Two communication towers located at v ∈ R2 and u ∈ R2 are sending directed signals to each other (it is only possible to hear
the signal when in its direct path). You are at the origin and want to travel the shortest possible distance to
intercept their signals. What vector specifies the distance and direction you must travel to intercept their signals?
We can solve this problem by recognizing that the closest point to the origin on the line along which the signals can be intercepted is the vector that is orthogonal to the line (i.e., it is the orthogonal projection of the origin onto the
line). The definition of the line is:
| = | | { a ⋅ (u - v) + v | a ∈ R}
|
|
Thus, the point p ∈ R2 to which we want to travel must be both on the line and orthogonal to the
line (i.e., its slope must be orthogonal to any vector that represents the slope of the line, such as u - v). In other words, it must satisfy the following two equations:
Thus, it is sufficient to solve the above system of equations for p.
4. Vector Spaces
We are interested in studying sets of vectors because they can be used to model sets of system states, observations
and data that might be obtained about systems, geometric shapes and regions, and so on. We can then represent real-world problems
(e.g., given some observations, what is the actual system state) as equations of the form M ⋅ v = w, and sets of vectors as
the collections of possible solutions to those equations. But what is exactly the set of possible solutions to M ⋅ v = w?
Can we characterize it precisely? Can we define a succinct notation for it? Can we say anything about it beyond simply solving the equation?
Does this tell us anything about our system?
In some cases, it may make more sense to consider only a finite set of system states, or an infinite set of discrete states (i.e., only
vectors that contain integer components); for example, this occurs if vectors are used to represent the number of atoms, molecules, cows, chickens,
power plants, single family homes, and so on. However, in this course, we make the assumption that our our sets
of system states (our models of systems) are infinite and continuous (i.e., not finite and not discrete); in this context, this simply
means that the entries in the vectors we use to represent system states are real numbers.
Notice that the assumption of continuity means that, for example, if we are looking for a particular state (e.g., a state corresponding
to some set of observations), we allow the possibility that the state we find will not correspond exactly to a state that "makes sense". Consider
the example problem involving the barn of cows and chickens. Suppose we observe 4 heads and 9 legs. We use the matrix that
represents the relationships between the various dimensions of the system to find the number of cows and chickens:
Notice that the solution above is not an integer solution; yet, it is a solution to the equation we introduced because the set of system states
we are allowing in our solution space (the model of the system) contains all vectors in R2, not just those with integer entries.
As we did with vectors and matrices, we introduce a succinct language (consisting of symbols, operators, predicates, terms, and formulas) for
infinite, continuous sets of vectors. And, as with vectors and matrices, we study the algebraic laws that govern these symbolic expressions.
4.1. Sets of vectors and their notation
We will consider three kinds of sets of vectors in this course; they are listed in the table below.
| kind of set (of vectors) |
maximum
cardinality
("quantity of
elements") |
solution space of a... |
examples |
| finite set of vectors |
finite |
|
- {(0,0)}
- {(2,3),(4,5),(0,1)}
|
| vector space |
infinite |
homogeneous system of
linear equations:
M ⋅ v = 0 |
- {(0,0)}
- R
- R2
- span{(1,2),(2,3),(0,1)}
- any point, line, or plane
intersecting the origin
|
| affine space |
infinite |
nonhomogeneous
system of
linear equations:
M ⋅ v = w |
- { a + v | v ∈ V} where
V is a vector space and a is a vector
- any point, line, or plane
|
To represent finite sets of vectors symbolically, we adopt the convention of simply listing the vectors between a pair of braces (as with any
set of objects). However, we need a different convention for symbolically representing vector spaces and affine spaces. This is because we
must use a symbol of finite size to represent a vector space or affine space that may contain an infinite number of vectors.
If the solution spaces to equations of the form M ⋅ v = w are infinite, continuous sets of vectors, in what way can be characterize them?
Suppose that M ∈ R2×2 and that is M invertible. Then we have that:
| = | | | = | | | = | | | = | | | = | | | = | | (s/(ad−bc)) ⋅ | | + (t/(ad−bc)) ⋅ | |
|
|
Notice that the set of possible solutions v is a linear combination of two vectors in R2. In fact, if a collection of solutions
(i.e., vectors) to the equation M ⋅ v = 0 exists, it must be a set of linear combinations (in the more general case of
M ⋅ v = w, it is a set of linear combinations with some specified offset). Thus, we introduce a succinct notation
for a collection of linear combinations of vectors.
Definition: A span of a set of vectors { v1, ..., vn } is the set of all linear combinations of vectors in { v1, ..., vn }:
| span { v1, ..., vn } = { a1 ⋅ v1 + ... + an ⋅ vn | a1 ∈ R, ..., an ∈ R }
|
|
Example: For each of the following spans, expand the notation into the equivalent set comprehension and determine if the set
of vectors is a point, a line, a plane, or a three-dimensional space.
- The set defined by:
The above span is a line.
- The set defined by:
The above span is a line.
- The set defined by:
The above span is a plane.
- The set defined by:
The above span is a set containing a single point (the origin).
- The set defined by:
| = | | {a ⋅ | | + b ⋅ | | + c ⋅ | | | a,b,c ∈ R}
| |
| = | |
The above span is a three-dimensional space.
Example: Using span notation, describe the set of vectors that are orthogonal to the vector [ 1 ; 2 ] ∈ R2.
We know that the set of vectors orthogonal to [ 1 ; 2 ] can be defined as the line L where:
It suffices to find a vector on the the line L. The equation for the line is:
We can choose any point on the line y = (-1/2) x; for example, [ 2 ; -1 ]. Then, we have that:
Example: Using span notation, describe the set of solutions to the following matrix equation:
Notice that the above equation implies two equations:
In fact, the second equation provides no additional information because 2 ⋅ [ 1 ; 2 ] = [ 2 ; 4 ]. Thus, the solution space
is the set of vectors:
We can now use our solution to the previous problem to find a span notation for the solution space:
Example: Suppose also that system states are described by vectors v ∈ R3 with the following units for each dimension:
| = | | | | | | x # carbon atoms | | y # hydrogen atoms | | z # oxygen atoms |
| |
|
|
|
Individual molecules are characterized using the following vectors:
| C3H8: | | , O2: | | , CO2: | | , H2O: | |
|
|
-
Suppose that a mixture contains only molecules of water (H2O) and carbon dioxide (CO2).
Using the span notation, specify the possible set of system states that satisfy these criteria.
The possible set of system states for the mixture is:
Recall that the above set is continuous. In this particular problem, only vectors with integer components
would be of interest; thus, the above set is at least guaranteed to contain all possible system states that satisfy
the specified criteria.
Then, if we wanted to solve a more constrained problem that satisfies the above criteria, we would know that we should only
consider vectors v ∈ V as possible solutions.
-
Suppose we observe the following system state (in terms of the number of each kind of atom):
How can we determine whether the above mixture could contain only H20 and CO2?
-
Suppose we want to know if a mixture of only C3H8 and O2 can ever react to produce a mixture of only CO2 and H2O.
How can we represent this as an equation of spans? This problem can be represented as follows:
Recall the definition for what constitutes a vector space (there are many equivalent definitions).
Definition: A vector space is a set of vectors that contains 0, is closed under vector addition and scalar multiplication, and is
such that all the elements in the set satisfy the vector space axioms governing vector addition and scalar multiplication.
Fact: Any set of linear combinations of a collection of vectors is closed under vector addition and scalar multiplication, contains
0, and satisfies the vector space axioms. In other words, for any collection of vectors v1, ..., vn, span{v1, ..., vn} is a vector space.
Fact: For any set of vectors V ⊂ Rn that satisfies the vector space axioms, there exists a finite set of at most n vectors
v1, ..., vk (where k ≤ n) such that span{v1, ..., vk} = V.
Given the two facts above, we can safely adopt span{v1, ..., vn} as a standard notation for vector spaces. In addition to this notation,
we will also often use the notation Rn for specific values of n (e.g., R2 is equivalent to span{[1;0],[0;1]}), and {0} for specific
vector 0 (e.g., {[0;0]} is equivalent to span{[0;0]}).
4.2. Membership and equality relations involving sets of vectors
Recall that many of the algebraic laws we saw governing operators on vectors and matrices involved equality of vectors and matrices. In fact, one
can view these laws as collectively defining the semantic equality of the symbols (i.e., they specify when two symbols refer to the same
object).
The meaning of symbols is closely tied to the equality relation we define over them. In the case of the span notation, one potential
problem is that there is more than one way to describe a set using span notation. For example:
How can we determine if two spans are equivalent? We must define the equality relation (i.e., the relational operator) that applies
to sets of vectors (including infinite sets containing all linear combinations of vectors). We first recall the definition of equality
for our vector notation.
Fact: Recall that two vectors v, w ∈ Rn are equal if and only if their components are equivalent:
| iff | |
a1 = b1 and a2 = b2 and ... and an = bn
|
|
With the equality of pairs of vectors defined, it is possible to provide a definition of equality for sets of vectors (both finite and infinite).
However, we will build the definition gradually. First, let us define when a vector is a member of a finite set of vectors using
vector equality.
Fact: A vector v ∈ Rn is a member of the finite set of vectors { w1, ..., wk } ⊂ Rn if it is equivalent to one of the
vectors in the set:
| iff | |
∃ w ∈ { w1, ..., wk } s.t. v = w
|
|
Notice that the above defines membership of v in the set using an equation (in this case, v = wi where i ∈ {1,...,k}). We can
take the same approach in the case of an infinite set of vectors.
Fact: A vector v ∈ Rn is a member of the set of vectors span { w1, ..., wk } ⊂ Rn if it is equivalent to one of the
vectors in the set:
| iff | | ∃ w ∈ span { w1, ..., wk } s.t. v = w |
| | iff | | ∃ w ∈ { a1 ⋅ w1 + ... + ak ⋅ wk | a1 ∈ R, ..., an ∈ R } s.t. v = w |
| | iff | | ∃ a1 ⋅ w1 + ... + ak ⋅ wk ∈ span { w1, ..., wk } s.t. v = a1 ⋅ w1 + ... + ak ⋅ wk |
| | iff | | ∃ a1 ∈ R ,..., an ∈ R s.t. v = a1 ⋅ w1 + ... + an ⋅ wn |
| | iff | | |
Thus, we can determine membership of a vector in a span by solving a matrix equation of the form M ⋅ u = v.
Example: Determine whether the following formula is true:
We proceed as in the fact above:
| iff | | ∃ w ∈ span { | | , | | } s.t. | | = w |
| | iff | | ∃ w ∈ { a ⋅ | | + b ⋅ | | | a ∈ R, b ∈ R } s.t. | | = w |
| | iff | | ∃ a ⋅ | | + b ⋅ | | ∈ span { | | , | | } s.t. | | = a ⋅ | | + b ⋅ | | |
| | iff | | ∃ a ∈ R, b ∈ R s.t. | | = a ⋅ | | + b ⋅ | | |
| | iff | | |
Since a solution to the matrix equation exists, the formula is true:
Example: Solve each of the following problems.
- Determine whether the following formula is true or false:
- Define the following line using span notation:
Now suppose we want to determine if a finite set of vectors is a subset of a span. Let us first consider how we would check if a
finite set of vectors is a subset of another finite set of vectors.
Fact: A finite set of vectors { v1, ..., vj } ⊂ Rn is a subset of the finite set of vectors { w1, ..., wk } ⊂ Rn if every
member of { v1, ..., vj } is a member of { w1, ..., wk }:
| { v1, ..., vj } ⊂ { w1, ..., wk }
| |
| iff | |
∀ v ∈ { v1, ..., vj }, ∃ w ∈ { w1, ..., wk } s.t. v = w
|
|
Thus, we can generalize the above by replacing the second finite set of vectors with a span.
Fact: A finite set of vectors { v1, ..., vj } ⊂ Rn is a subset of the set of vectors span { w1, ..., wk } ⊂ Rn if every
member of { v1, ..., vj } is a member of span { w1, ..., wk }:
| { v1, ..., vj } ⊂ span { w1, ..., wk }
| |
| iff | | ∀ v ∈ { v1, ..., vj }, ∃ w ∈ span { w1, ..., wk } s.t. v = w |
| | iff | | ∀ v ∈ { v1, ..., vj }, ∃ | | ∈ Rk s.t. | | ⋅ | | = v |
| | iff | | ∃ | | | | a11 | ... | a1j | | ⋮ | | ⋮ | | a1k | ... | akj |
| |
|
∈ Rk × j
s.t.
| |
⋅ | | | | a11 | ... | a1j | | ⋮ | | ⋮ | | a1k | ... | akj |
| |
|
= | | |
| |
Fact: For any finite set of vectors { v1, ..., vj } ⊂ Rn, for any real number scalars a1 ∈ R, ..., aj ∈ R,
we have that:
| { v1, ..., vj } ⊂ span { w1, ..., wk } implies a1 ⋅ v1 + ... + aj ⋅ vj ∈ span { w1, ..., wk }
|
|
We can see the above is true, because:
| = | | s11 ⋅ w1 + ... + sk1 ⋅ wk |
| | ⋮ | | | = | | s1j ⋅ w1 + ... + skj ⋅ wk |
| | = | | (a1 s11) ⋅ w1 + ... + (a1 sk1) ⋅ wk |
| | ⋮ | | | = | | (aj s1j) ⋅ w1 + ... + (aj skj) ⋅ wk |
| | = | | (a1 s11 + ... + aj s1j) w1 + ... + (a1 sk1 + ... + aj skj) wk
|
|
Thus, we have that:
| { v1, ..., vj } ⊂ span { w1, ..., wk } implies span { v1, ..., vj } ⊂ span { w1, ..., wk }
|
|
Definition: Using facts about sets,
we can then specify the following definition of equality between two spans for two finite sets of vectors V ⊂ Rn and
W ⊂ Rn:
| iff | | span W ⊂ span V and span V ⊂ span W
|
|
Example: Determine whether the following formula is true:
It suffices to set up two matrix equations and determine if solutions A ∈ R2 × 3 and B ∈ R3 × 2
exist:
Alternatively, we can check each vector individually (this is analogous to considering the above equations for A and B one column at a time).
| Is | | a linear combination of | | , | | , and | | ? |
| |
Is | | a linear combination of | | , | | , and | | ? |
| |
Is | | a linear combination of | | and | | ? |
| |
Is | | a linear combination of | | and | | ? |
| |
Is | | a linear combination of | | and | | ?
|
|
If all of the above are true, then the two spans are equivalent. If any of the above is false, then the two spans are not equivalent.
The above implies that a matrix can be used to represent a particular vector space. We will see in other sections
further below that a given vector space can be represented in more than one way by a matrix, and that more than one matrix can be used
to represent a vector space.
Definition: Given two vector spaces W and V, we have:
W is a (vector) subspace of V iff V ⊂ W.
4.3. Vector spaces as abstract structures
Our definitions of a vector space so far have explicitly referenced sets of concrete vectors as we usually understand them. However, this is not
necessary.
Definition: A vector space is a set of objects X that satisfies the following conditions:
- addition ⊕: X × X → X is an operation on elements of X such that:
- X is closed under ⊕, so for any x,y ∈ X:
- ⊕ is commutative and associative; for any x,y,z ∈ X, we have:
- there is a unique additive identity 0 ∈ X for the operation ⊕ where for any x ∈ X:
- every element x ∈ X has an additive inverse -x where:
- scalar multiplication ⊗: R × X → X is an operation on elements of X such that:
- X is closed under ⊗, so for any s ∈ R, x ∈ X:
- 1 ∈ R is an identity with ⊗, so for any x ∈ X:
- ⊗ is associative, so for any s, t ∈ R, x ∈ X:
- ⊗ distributes across ⊕, so for any x,y ∈ X:
The above definition specifies conditions under which any set of objects S can be studied as a vector space.
We have encountered many sets that satisfy the above properties (thus making them vector spaces); below is a table of vector spaces,
including vector spaces we have already encountered and vector spaces we will encounter later in the course.
| vector space |
addition
operation |
additive
identity |
scalar
multiplication
operation |
| R |
addition of
real numbers |
0 |
multiplication of
real numbers |
| R2 |
vector addition:
[ a ; b ] + [ c ; d ] = [ a + c ; b + d ]
|
[ 0 ; 0 ] |
scalar multiplication:
s ⋅ [ a ; b ] = [ s ⋅ a ; s ⋅ b ]
|
| R3 |
vector addition:
[ a ; b ; c ] + [ d ; e ; f ] =
[ a + d ; b + e ; c + f ]
|
[ 0 ; 0 ; 0] |
scalar multiplication:
s ⋅ [ a ; b ; c ] = [ s ⋅ a ; s ⋅ b ; s ⋅ c ]
|
| Rn |
vector addition:
[ a1 ; ... ; an ] + [ b1 ; ... ; bn ] =
[ a1 + b1 ; ... ; an + bn ]
|
[ 0 ; ... ; 0 ] |
scalar multiplication:
s ⋅ [ a1 ; ... ; an ] = [ s ... a1 ; ... ; s ⋅ an ]
|
| span { [0;0] } = { [0;0] } |
vector addition
|
[0;0] |
scalar multiplication
of vectors in R2
|
| span { v1 , ... , vk } ⊂ Rn |
vector addition
|
[ 0 ; ... ; 0 ] |
scalar multiplication
of vectors in Rn
|
| R2×2 |
matrix addition
|
[ 0 , 0 ; 0 , 0 ] |
scalar multiplication
of a matrix
|
| Rn×n |
matrix addition
|
[ 0, ..., 0 ; ... ; 0, ..., 0 ] |
scalar multiplication
of a matrix
|
affine space with
origin at a ∈ R2 |
v ⊕ w = (v - a) + (w - a) + a
|
a |
s ⊗ v = s ⋅ (v - a) + a
|
set of lines
through the origin
f(x) = a x |
f ⊕ g = h
where h(x) = f(x) + g(x)
|
f(x) = 0 ⋅ x |
s ⊗ f = h
where h(x) = s × f(x)
|
set of polynomials
of degree 2
f(x) = a x2 + b x + c |
f ⊕ g = h
where h(x) = f(x) + g(x)
|
f(x) = 0 |
s ⊗ f = h
where h(x) = s × f(x)
|
set of polynomials
of degree k
f(x) = ak xk + ... + a0 |
f ⊕ g = h
where h(x) = f(x) + g(x)
|
f(x) = 0 |
s ⊗ f = h
where h(x) = s × f(x)
|
Example: The affine space A = { a + v | v ∈ V} is a vector space for appropriate definitions of addition, scalar multiplication, and identity.
An abstract definition of vector spaces is useful because it also allows
us to study by analogy and learn about other objects that are not necessarily sets of vectors. All the properties we can derive about vector
spaces using the above definition will apply to other sets of objects that also satisfy the above definition.
Example: We consider the set of functions F = { f | f( x) = cx, c ∈ R}. How do we show that F is a vector
space?
Example: Show that F = { f | f( x) = bx2 + cx, b, c ∈ R} is a vector space.
For our purposes, it is sufficient to show that there is an additive identity, that the set is closed under addition, and that the set is closed under
scalar multiplication. There is an additive identity:
The set is closed under the usual addition operation on polynomial curves; for any f, g ∈ F we have f + g = h where:
| = | | | = | | | = | | (bx2 + cx) + (b'x2 + c'x) |
| | = | | (b + b') ⋅ x2 + (c + c') ⋅ x |
| | = | | (b + b') ⋅ x2 + (c + c') ⋅ x |
| | ∈ | |
For any f ∈ F and s ∈ R we have h = s ⋅ f where:
Example: Find two elements in F = { f | f( x) = bx2 + cx + d, b, c, d ∈ R} that are linearly independent. What does it mean for
two functions to be linearly independent?
Two vectors g, h ∈ \F are linearly independent if they are not linearly dependent. This means there exists no scalar such that
s ⋅ g = h or s ⋅ h = g. One example of such a pair would be:
There is no single scalar by which we can multiply the curve h( x) = 1 to obtain a parabola, and there is no single scalar by which we can
multiply the parabola to obtain a non-zero flat line.
Example: What is a finite set of functions that spans { f | f( x) = bx2 + cx + d, b, c, d ∈ R}? One such set is:
{f,g,h} where f(x) = 1, g(x) = x, h(x) = x2
Example: We consider the set of functions { f | f( x) = x k, k ∈ R}. The following definitions of addition and scalar multiplication
make this set of functions a vector space.
Fact: Once we start thinking of curves as a vector space, we can rewrite curve-fitting problems as equations involving linear combinations of
curves. For example, suppose we have some curve φ for which we do not know the formula...
...that represents some observable phenomenon. We can hypothesize that
the curve φ( x) is a linear combination of simpler curves, such as f( x) = x and g( x) = x2. This is equivalent to
hypothesizing that φ is in the following vector space:
| span {f, g} = { f | f(x) = a x2 + b x where a,b ∈ R }
|
|
We can then set up the following
equation:
However, the above equation cannot directly be solved for a, b ∈ R because we do not know the formula for φ. Suppose we can sample
φ on some finite collection of input values { x1,..., xm } ⊂ R.
We can then write an equation that approximates the above equation at those
points:
The above is equivalent to the following system of equations:
It can also be rewritten as the following matrix equation:
| | | | | f(x1) | g(x1) | | ⋮ | | f(xm) | g(xm) |
| |
| ⋅ | | | |
| = | |
Notice that because we know f and g exactly, the matrix above has all constant entries. Furthermore, the right-hand side of the equation also
consists of a vector with all constants as entries because we assumed we can sample φ on those inputs. Thus, we now have a matrix equation of
the form M ⋅ v = w.
We can now use rref computation or, if the matrix is invertible, any other method for computing the matrix inverse to solve
the above equation for a,b ∈ R. This would give us the exact coefficients of a curve in span {f, g} that fits φ at the x values { x1,...,xm }.
Fact: For any two natural numbers k, m ∈ N where k ≠ m, the curves f and g defined below are linearly independent:
Corollary: For any natural number k ∈ N, the curves f and g defined below are linearly independent:
We can see this by choosing any set of real number inputs { x1,..., xk+2 }; the equation below then has no solution s ∈ R:
Since no such s exists, f and g must be linearly independent.
Example: Suppose we have the following two curves:
If we choose any three inputs, e.g., {1,2,3}, we will find that g cannot be a linear combination of f because the three points will not be collinear.
Since we derived a contradiction above, no such s exists, so f and g must be linearly independent.
Fact: For any collection of exactly k points in R2:
there exists a polynomial f( x) = ak-1xk-1 + ... + a1 x + a0 that fits those points exactly.
We know the above must be true because the columns of the following matrix in Rk × k must be linearly independent:
| | | | | (x1)k-1 | ... | (x1) | 1 | |
⋮ | | ⋮ | ⋮ | |
(xk)k-1 | ... | (xk) | 1 |
| |
|
|
|
This means that the equation below must have a unique solution:
| | | | | (x1)k-1 | ... | (x1) | 1 | |
⋮ | | ⋮ | ⋮ | |
(xk)k-1 | ... | (xk) | 1 |
| |
| ⋅ | |
| |
| = | |
Example: Just as with any vector space, we can set up and solve problems involving linear combinations of vectors. Suppose we want to find a
function in the space { f | f( x) = ax3 + bx2 + cx + d, a, b, c, d ∈ R} that fits a certain collection of points, such as:
{(1,3), (-1,13), (2,1), (-2,33)}
We can interpret each point as a pair (x, f(x)). We can then set up the following system of equations:
Expanding, we have:
| = | | |
a(-1)3 + b(-1)2 + c(-1) + d | |
| = | | | = | | |
a(-2)3 + b(-2)2 + c(-1) + d | |
| = | | |
Notice that we can rewrite this in the form of an equation M v = w:
| | | | | (1)3 | (1)2 | (1) | 1 | | (-1)3 | (-1)2 | (-1) | 1 | | (2)3 | (2)2 | (2) | 1 | | | | (-2)3 | (-2)2 | (-2) | 1 |
| |
|
⋅ | | | |
| = | |
This shows us that we can interpret individual objects in {f | f(x) = ax3 + bx2 + cx + d, a,b,c,d ∈ R} as vectors in R4.
We can also view this problem in terms of systems, system states, and observations. If the function f(x) = ax3 + bx2 + cx + d that solves
the above system is a state of the system, then (3, 13, 1, 33) is a partial observation of that state along four distinct "dimensions".
Note that finding the equation for a line that crosses two points is just a special case of the above.
Example: We want to find a function f( x) = cx + d such that the points (2,3) and (5,-4) fall on the line the equation represents. Thus,
we have:
We can consider many spaces of functions beyond spaces of polynomial functions. For example, suppose exp(x) = ex.
Then we can define the following vector space:
span{ exp, cos , sin }.
We can also generalize this approach to families of related functions.
Example: Consider the following set of vectors of functions, where f' denotes the derivative of a function f:
F = { (f, f, f') | f(x) = bx2 + cx + d }
The set F is a vector space. Now, suppose we have the following problem. Find the function for a parabola in F such that
(1,4) and (2,-3) lie on the parabola, and the maximum or minimum point on the parabola is at x = 1. Such a function is
represented by the solution to the following equation:
| | | | | (1)2 | (1) | 1 | | (2)2 | (2) | 1 | | 2(1) | 1 | 0 |
| |
| ⋅ | | | |
| = | |
Note that the number of rows in the matrix (and result vector) corresponds to the number of data points for which
a model is being sought, and is not bounded.
Example: Find the order 5 polynomial that exactly fits the following points in R2:
We must first compute the vectors that approximate each of the following curves that span our space of possible polynomials
at each of the x components of the points above:
| { f | f(x) = a5 x5 + a4 x4 + a3 x3 + a2 x2 + a1 x + a0 + % where ai ∈ R }
| |
| = | |
where
Thus, we want to solve for the coefficients of the following linear combination of curves:
| a5 f + a4 g + a3 h + a2 i + a1 j + a0 l | |
| = | | curve represented by data points
|
|
Thus, we would have the following approximation of the above linear combination at the specific x values in { -1, 8, 6, 2, -10, 15 }:
| a5 | | | | f(-1) | | f(8) | | f(6) | | f(2) | | f(-10) | | f(15) |
| |
| +
a4 | | | | g(-1) | | g(8) | | g(6) | | g(2) | | g(-10) | | g(15) |
| |
| +
a3 | | | | h(-1) | | h(8) | | h(6) | | h(2) | | h(-10) | | h(15) |
| |
| +
a2 | | | | i(-1) | | i(8) | | i(6) | | i(2) | | i(-10) | | i(15) |
| |
| +
a1 | | | | j(-1) | | j(8) | | j(6) | | j(2) | | j(-10) | | j(15) |
| |
| +
a0 | | | | l(-1) | | l(8) | | l(6) | | l(2) | | l(-10) | | l(15) |
| |
|
| |
| = | |
We can convert the above into the following matrix equation:
| | | | | f(-1) | g(-1) | h(-1) | i(-1), | j(-1) | l(-1) | |
f(8) | g(8) | h(8) | i(8), | j(8) | l(8) | |
f(6) | g(6) | h(6) | i(6), | j(6) | l(6) | |
f(2) | g(2) | h(2) | i(2), | j(2) | l(2) | |
f(-10) | g(-10) | h(-10) | i(-10) | j(-10) | l(-10) | |
f(15) | g(15) | h(15) | i(15) | j(15) | l(15) |
| |
|
⋅
| |
| |
| = | |
It is then sufficient to solve the above equation to obtain the ceofficients, and thus the degree 5 polynomial that exactly fits the points
above.
The disadvantage to using the approach presented in this subsection to fitting functions to data points is that the data must
match an actual function perfectly (or, equivalently, the space of functions being considered must be rich
enough to contain a function that can fit the data points exactly). We will see further below
how to find functions that have the "best" fit (for one particular definition of "best") without necessarily matching the points exactly.
Example: Let polynomials in F = { f | f( t) = a t2 + b t + c } represent a space of possible radio signals.
To send a vector v ∈ R3 to Bob, Alice sets her device to generate the signal corresponding to the polynomial in F whose coefficients
are represented by v.
Bob can then let his radio receiver sample the radio signals in his environment at multiple points in time t to retrieve the message.
Suppose Alice wants to transmit the following vector v ∈ R3 to Bob:
Alice sets her radio transmitter to generate a signal whose amplitude as a function of time is:
How can Bob recover the message Alice is sending?
Bob can recover the message by having his device sample the signal at three points, e.g., t1 = 1, t2 = 2, and t3 = 3.
Once Bob does this, he can set up an equation to recover the curve Alice used to generate the signal:
| | | | | (1)2 | (1) | 1 | | (2)2 | (2) | 1 | | (3)2 | (3) | 1 |
| |
| ⋅ v | |
| = | | | = | |
The above equation can then be solved to obtain Alice's message v.
4.5. Basis, dimension, and orthonormal basis of a vector space
We have adopted span{v1,...,vn} as our notation for vector spaces. However, this makes it possible to represent a given vector space
in a variety of ways:
span{(0,1),(1,0)} = span{(0,1),(1,0),(1,0)} = span{(0,1),(1,0),(1,0),(1,0)}, and so on.
We might naturally ask: given
a vector space V, what is the smallest possible size for a finite set of vectors W such that V = span W?
Definition: A finite set of vectors B is a basis of the vector space V if span B = V and for all finite
sets of vectors W such that span W = V, |B| ≤ |W|.
Fact: A finite set of vectors v1,...,vn is a basis for V iff span {v1,...,vn} = V and the vectors v1,...,vn
are setwise linearly independent.
Fact: Given a finite set of vectors v1,...,vn, we can find the basis for span {v1,...,vn} by creating a matrix M in which the
rows are the vectors v1,...,vn and computing rref M. The set of distinct nonzero rows in rref M is a basis for span {v1,...,vn}.
Example: We can find the basis of V = span {[-3;0;7;0], [-9;0;21;0], [0;0;2;8], [0;0;1;4], [3;0;13;4], [0;0;1;0]} by computing
the reduced row echelon form of the following matrix. We can use a third-party tool to do so (e.g.,
WolframAlpha).
| = | | | | | | -3 | 0 | 7 | 0 | | -9 | 0 | 21 | 0 | | 0 | 0 | 2 | 8 | | 0 | 0 | 1 | 4 | | 3 | 0 | 13 | 4 | | 0 | 0 | 1 | 0 |
| |
| |
| | = | | | | | | 1 | 0 | 0 | 0 | | 0 | 0 | 1 | 0 | | 0 | 0 | 0 | 1 | | 0 | 0 | 0 | 0 | | 0 | 0 | 0 | 0 | | 0 | 0 | 0 | 0 |
| |
| |
| |
The rows of the matrix rref M will correspond to the vectors in a basis for V. Thus, we have that:
Definition: The dimension of a vector space V, which we write as dim V, is the size of any basis of V (recall that every basis
is the same size as every other basis, since they all must have the smallest size of any set of vectors that spans V).
Example: What is the dimension of { f | f( x) = ax3 + bx2 + cx + d, a, b, c, d ∈ R}?
The dimension of a space is the size of its basis.
A basis must consist of vectors that are linearly independent from one another, and it must span the space. We know that the following set B
spans the space:
We also know that the curves f, g, h, and l are linearly independent. Thus, B is a basis. Since | B| = 4 and span B = V, then we
have that:
Example: Consider the vector space V consisting of finite sets of real numbers:
What are the basis and dimension of this vector space?
The basis of the space is B = { {1} } since you can obtain any finite set of real numbers
by taking linear combinations of the set {1} ∈ V. Since span { {1} } = V and |{ {1} }| = 1, dim V = 1.
Definition: A finite set of vectors B is an orthonormal basis of the vector space V if B is a basis of V,
all the vectors in B are unit vectors, and the vectors in B are setwise orthogonal.
Recall that for any vector v ∈ Rn and any unit vector u ∈ Rn, (v ⋅ u) ⋅ u is the projection of v onto the line parallel to
u (i.e., the vector space {a u | a ∈ R}). We can use this fact to define a process for turning an arbitrary basis into an orthonormal basis.
Fact: Given a basis B = { v1,..., vn}, it is possible to turn it into an orthonormal basis { e1,..., en} by using the Gram-Schmidt process. This
algorithm can be summarized as follows.
| = | | | | | = | | | | | = | | v3 − ((v3 ⋅ e1) ⋅ e1) − ((v3 ⋅ e2) ⋅ e2) | |
| | | | = | | v4 − ((v4 ⋅ e1) ⋅ e1) − ((v4 ⋅ e2) ⋅ e2) − ((v4 ⋅ e3) ⋅ e3) | |
| | | | ⋮ | | | | | = | | vn − Σi = 1n-1 ((vn ⋅ ei) ⋅ ei) | |
| | |
Intuitively, for each vector vi ∈ B, the algorithm substracts out the contributions of the already-computed orthogonal unit vectors from
vi, obtaining ui, and then rescales ui to make it into a unit vector ei.
At the end of the above process, {e1,...,en} is the orthonormal basis (and {e1,...,en} is a basis of orthogonal vectors that are not
necessarily unit vectors).
Many computational environments for mathematics that support linear algebra provide an operator for turning a basis into an orthonormal basis.
Why is an orthonormal basis useful? Once again, we appeal to the fact that (v ⋅ u) ⋅ u is the projection of v onto u, where
v ⋅ u is the length of that projection. Suppose we want to determine how to express an arbitrary vector v using an orthonormal
basis u1,...,un.
Fact: Given a vector v ∈ Rn, and an orthonormal basis B = { u1,..., un} for Rn, we can determine what linear combination of the vectors
u1,..., un yields v by computing:
a = (MB)⊤ ⋅ v.
Notice that the components of the vector a, which we will call a1,...,an, are the scalars needed to compute v as a
linear combination of the vectors u1,...,un:
v = a1 u1 + ... + an un = MB a.
Fact: Given a vector v ∈ Rn, some k < n, and an orthonormal basis B = {u1,...,uk} for a subspace W ⊂ Rn,
the product (MB ⋅ (MB)⊤ ⋅ v) is the projection of v onto W.
Example: Notice the relationship of the above fact to projection onto the span of a single unit vector u = ( x, y) in R2.
Suppose we have a basis B = { u} for a subspace { s ⋅ u | s ∈ R2} ⊂ R2. Then we have:
Thus, for an arbitrary v ∈ R2 not necessarily in { s ⋅ ( x, y) | s ∈ R2} we have:
Thus, we see that the projection of a vector onto another unit vector in R2 is just a special case of the general approach to projection.
Example: Suppose we want to project the vector v ∈ R2 onto the space W ⊂ R2 where:
We compute the matrix MB and its transpose. MB is a 2 × 1 matrix in this case, and ( MB) ⊤ is a 1 × 2 matrix:
We can now apply the formula. Notice that it is equivalent to the formula for projection of v onto the single vector that spans W:
Thus, the projection of v onto W is [3; 3].
Example: Suppose we want to project the vector v ∈ R3 onto the space W ⊂ R3 where:
We compute the matrix MB and its transpose. MB is a 3 × 2 matrix in this case, and ( MB) ⊤ is a 2 × 3 matrix:
We can now apply the formula:
Thus, the projection of v onto W is [3; 3; 5].
Example: Suppose we want to project the vector v ∈ R3 onto the space W ⊂ R3 where:
What is the orthogonal projection of v onto W?
Since the two vectors that span W are already an orthonormal basis, we can simply project v onto the two individual vectors in the
orthonormal basis and take the sum to obtain the orthogonal projection of v onto W:
Example: Suppose we want to project the vector v ∈ R3 onto the space W ⊂ R3 where:
What is the orthogonal projection of v onto W?
Since the two vectors that span W are already orthogonal, it is sufficient to turn them into unit vectors in order to obtain an
orthonormal basis of W. We can then project v onto the two individual vectors in the
orthonormal basis and take the sum to obtain the orthogonal projection of v onto W:
| = | | span { | | , | | }
( | | ⋅ | | ) ⋅ | | + ( | | ⋅ | | ) ⋅ | |
| |
| = | | | = | |
4.6. Homogeneous, non-homogeneous, overdetermined, and underdetermined systems
While we have usually considered n × n matrices, in real-world applications (especially those involving data), system states usually have
a shorter description than the corpus of data (e.g., observational data) being used to determine the system state. Thus, problems in such applications
usually involve matrices in which the number of rows is very different from the number of columns. Furthermore, the data may be noisy,
which means that there may be no exact system state that matches the data. Informally, this might mean that the system of equations being
used to determine a system state is overdetermined. On the other hand, if the amount of data is not sufficient to determine a single system
state, a system is underdetermined.
Definition: For any matrix M ∈ Rn×m and vector v ∈ Rm, the system M x = v is overdetermined if there exist
no solutions to the equation M x = v.
Definition: For any matrix M ∈ Rn×m and vector v ∈ Rm, the system M x = v is undetermined if there exist
two or more solutions for x that satisfy the equation M x = v.
Definition: For any matrix M ∈ Rn×m, the system M x = 0 is homogeneous.
Definition: For any matrix M ∈ Rn×m and vector v ∈ Rm where v ≠ 0, the system M x = v is nonhomogeneous.
Fact: A homogeneous system M x = 0 has at least one solution.
Fact: A homogeneous system M x = 0 is never overdetermined.
Fact: The solution space of a homogeneous system is a vector space:
- there is a unique additive identity: 0 is a solution
- adding two solutions yields a solution:
- multiplying a solution by a scalar yields a solution:
Fact: The solution space of a nonhomogeneous system is an affine space.
Motivating Example: Suppose we have a nonhomogeneous system M x = v where v ∈ R1000000.
We may not know ahead of time whether or
not it is overdetermined. Suppose we do not want to incur the cost of attempting to solve M x = v exactly. This might be because we only want to make
one pass of the data to reduce costs, but it might also be because this is a data stream that is too voluminous to store, so the data will be
gone unless we solve the system right away (e.g., data from a telescope, a particle collider, or Twitter).
In such cases, we can typically assume the data will have noise, so the system is overwhelmingly likely to be overdetermined and have no solution.
Thus, we are okay with finding an approximate solution.
We do know, however, that M x = 0 has at least one solution, and that the solution space is a vector space (so, for example, we
could try to "search" for a better solution using some other technique involving addition and scalar multiplication
once we find at least one non-trivial one). Thus, we might instead
choose to solve the system M x = 0, knowing that even in the worst case, a very poor approximate solution of 0 will always be found
in the worst case.
Is there a better compromise between these two strategies of keeping v or changing it to 0? Can we find some other space of
solutions that won't be overdetermined, but will
still allow us to find a non-trivial (nonzero) approximate solution? One possibility is to project the vector v onto a subspace
of the solution space, ensuring that the system is no longer overdetermined. This approach is covered in the section below.
4.7. Application: approximating overdetermined systems
Fact: Suppose we have an overdetermined system where M ∈ Rm × n, v ∈ Rn, and w ∈ Rm:
Let us rewrite M in terms of its columns ci ∈ Rm:
Let B = { c1,..., cn} be a basis for span B ⊂ Rm. To be more general, we will use W = Rm and W' = span B:
Now, it is possible to restate the fact that M ⋅ v = w has no solution in a different way:
The above tells us that the real problem is that w ∉ span B. It also tells us that for any w' in the span of the columns of M (which we call span B), M ⋅ v = w' will have a solution:
| = | | | ∈ | | | = | | w' has at least one solution
|
|
Definition: Suppose we have an overdetermined system where v ∈ Rn, and w ∈ Rm:
We can find an approximate solution v' by picking some w' ∈ span { c1, ..., cn} and solving the new equation:
The error of the approximate solution v' is defined to be || w' − w||.
We see that we may have many choices for w' in changing an overdetermined system M ⋅ v = w to a system with at least one solution M ⋅ v' = w'.
Above, we have introduced a notion of error so that we can compare the quality of different choices of w'. How can we pick the w' that minimizes the
error ||w - w'||? Let us first define what the vector leading to the minimal error is.
Definition: Given w ∈ W and a subspace W' ⊂ W, the vector w' within the subspace W' that is closest to w is
a vector w* ∈ W' such that || w - w*|| is minimal. In other words, for all w' ∈ W,
||w - w*|| ≤ ||w - w'||.
How do we find w*?
Fact: We first review the triangle inequality in the case of a right triangle. Suppose we have a triangle with a height a, a base length of b, and
a hypotenuse of length c. Then we have:
This implies that the orthogonal projection of a vector v ∈ V onto a subspace W ⊂ V is the closest point in W to v.
Fact: Given w ∈ W and a subspace W' ⊂ W, the orthogonal projection w* of w onto W' is the closest vector in W' to w.
Fact: Suppose we are given an overdetermined system:
We assume the matrix can be written in terms of its columns:
The least-squares approximate solution to M ⋅ v = w is the solution v* to the equation:
where w* is the orthogonal projection of w onto span { c1, ..., cn}.
The solution v* is the one that leads to the smallest possible error for any possible vector v that we can multiply by M:
||w - M v*|| ≤ ||w - MB v||
Why is it called a "least-squares" approximate solution? In the table below, we summarize the correspondences used in the above facts.
concept related to
solving MB x = v |
notation |
relationship |
notation |
geometric concept |
the space of values W' with
which we can replace w in
the overdetermined system M v = w
to make a system M v = w'
that has solutions |
{M ⋅ v | v ∈ Rn} |
the span of the
columns of M |
span B |
the subspace W' of W
spanned by B |
the error of an approximate
solution v' |
||w - M v' || |
M v' = w' |
||w - w'|| |
the distance between
w ∈ W and w' ∈ span B |
M ⋅ v* where v* is
the minimum error solution |
for all v',
||w - M w* || ≤ ||w - M w' || |
M v* = w* |
for all w' ∈ span B,
||w - w*|| ≤ ||w - w'|| |
the orthogonal projection
w* of w ∈ W onto span B
(the closest vector in span B
to w) |
Notice that we know a solution to M v* = w* exists, and that we can show this in two different ways. Since w* ∈ span B, it
must be that w is a linear combination of the vectors in B, so it is a linear combination of the columns in M. Alternatively, if M is
a square matrix and we know that B is a basis, then the columns of M are linearly independent, which means M is invertible, so
v* = M -1 w*.
Fact: We can compute the least-squares approximate solution v* to any equation M ⋅ v = w by using the following process:
- break M up into a set of its column vectors
- find an orthonormal basis B of the span of the column vectors of M to make MB
- use MB to compute the projection w* of w onto span B
- solve the system M v* = w* (e.g., by finding the rref of an augmented matrix)
Example: Find the least-squares approximate solution v* to the following equation:
We have an overdetermined system (i.e., an equation with no solution) of the form M ⋅ v = w. We must turn it into an equation M ⋅ v = w*
that does have a solution by replacing w with w*, the orthogonal projection of w that is in the span of the columns of M.
Let W be the span of the columns of the matrix in the equation above:
We first need to find an orthonormal basis of W. Since the two vectors above are already orthogonal, it is sufficient to normalize them.
More generally, we would need to apply the Gram-Schmidt process (this is technically what we are doing here, it is just that the terms
we need to subtract are always 0 in this case). Thus, we have an orthonormal basis:
We now compute the orthogonal projection of w to find w* ∈ W:
Thus, we now have a solvable equation M ⋅ v = w*:
The error of the approximate solution is || w − w*||:
| error of the approximate solution | | | |
| = | | | = | | | = | | | = | |
Example: Suppose a matrix M is such that M ⋅ v = 0 has exactly one solution. What can we say about the error of the least-squares
approximation of any system M ⋅ v = w?
Since M is invertible (because there is exactly one solution to M ⋅ v = 0), then there is always an exact solution v to M ⋅ v = w:
Thus, the columns of M are linearly indepenent and span the space of all possible vectors that can appear on the right-hand side of the equation.
This means that w* = w, so the error is || w − w*|| = || w − w||| = 0.
Example: Suppose a matrix M is such that M ⋅ v = 0 has Rn as its space of solutions. What can we say about any system M ⋅ v = w?
What can we say about the error of any least-squares approximation of a solution for M ⋅ v = w?
This means that M is the matrix consisting of all zeroes. Thus, the span of its columns is { 0 }, the set consisting of only the origin. Thus, the error of
any approximate solution will be ||w - 0|| = ||w||.
Example: We saw that if M is the matrix consisting of all zero entries, w* must be the zero vector (i.e,. the origin). Are there other
matrices M for which w* will be 0?
Yes, if all the columns of M are orthogonal to w, then the orthogonal projection of w onto the span of the columns of M will be the origin, 0.
For example, consider the following overdetermined system:
Since [−2; 1] ⋅ [1; 2] = 0 and [−2; 1] ⋅ [2; 4] = 0, the orthogonal projection of [−2; 1] onto the span of the two columns will be [0; 0].
Relationship to curve fitting and linear regressions in statistics
The method described above does overlap with standard curve fitting and linear regression techniques you see
in statistics. There are many variants to these approaches, and the one considered above corresponds to a fairly
basic variant that has no specialized characteristics (i.e., it makes no special assumptions about the data points,
the relative importance of the data points, their distribution, or the way they can be interpreted).
-
The approach above is known as
ordinary least squares and as
linear least squares.
-
The case in which the function space is {f | f(x) = ax + b, a,b ∈ R}
corresponds to a simple linear regression.
This involves fitting a line to a collection of points while minimizing the sum of the squares of the
distances parallel to the y-axis between all the data points and the approximate line.
This diagram
is an illustration of this. The method in these notes is more general in that it is not restricted to
polynomials of order 1, but can be used to fit polynomials of any order to data.
-
We can restate the least squares method described in these notes as finding x* such that
the vector ε in M x* = v - ε is minimized. Notice that ε + w = v.
The length of the vector ε can be viewed as the sum of squares of y-axis-aligned distances from the
estimate curve to the actual data points:
||ε|| = ||v - M x*||.
-
This diagram illustrates the
projection method being used.
-
The matrix M in M x = v is sometimes called the
design matrix.
The same term is used to refer to the
corresponding
matrix in a simple linear regression.
4.8. Application: approximating a model of system state dimension relationships
The approach described in the previous section can be used to approximate a solution to the equation M v = w. Usually, if M describes
a model of a system (in this sense, system refers to a system of states that are described by values along some number of dimensions),
solving M v = w corresponds to determining a system state v given some other information about a system state w.
What if we instead have a large collection of pairs of observations of system states of the form (v,w) (or, more generally, any collection of
observations of a system along multiple dimensions). Can we approximate a model of a set of relationships between some two subsets of the
dimensions in the system? In other words, if we take all our observations (x1, ..., xn) and divide them into pairs of descriptions
x = (x1,...,xk) and v = (xk+1,...,xn), can we find the best M that approximates the relationship between incomplete
system state descriptions x and v?
Example: Suppose we have the following dimensions in our system:
- number of red dwarf stars
- number of G type stars
- number of pulsars
- units of infrared (IR) radiation observed
- units of ultraviolet (UV) radiation observed
- units of gamma (γ) radiation observed
Suppose that we already have some set of confirmed (but possibly noisy) observations of systems along all the dimensions (the dimensions
of the quantities in each point correspond to the list of dimensions above):
For the above observations, we want to find a matrix that relates the first three dimensions (the number of each type of star) to the last
three dimensions (the amount of each kind of radiation). In other words, we are looking for a matrix M ∈ R3× 3 of the
form:
| | | | a units IR/red dwarf | b units IR/G type | c units IR/pulsar | |
d units UV/red dwarf | e units UV/G type | f units UV/pulsar | |
g units γ/red dwarf | h units γ/G type | i units γ/pulsar |
| |
|
Multiplication by the above matrix represents a system state description transformation with the following units:
(# red dwarf stars, # G type stars, # pulsars)
→ (units IR, units UV, units γ)
We can split the data into two collections of points: those that specify the number of each type of star (the inputs to the above transformation),
and those that specify the amount of each kind of radiation (the output of the above transformation). Below, we call these P and Q. We then
turn these two sets of data points into matrices. In order to turn this problem into the familiar form M v = w, we can transpose the two
matrices.
Example: Suppose we have four dimensions in our system. Also, suppose that we already have some set of
confirmed (but possibly noisy) observations of systems along all the dimensions (the dimensions
of the quantities in each point correspond to the list of dimensions above):
For the above observations, we want to find a matrix that relates the first two dimensions to the last
two dimensions. We would then set up the following equations:
Unfortunately, there is no single solution a, b, c, d ∈ R to the above collection of equations.
To find an approximate solution, we can convert the above into a single matrix equation:
We can go further and turn this into an equation of the form M ⋅ v = w:
| | | | | 1 | 0 | 0 | 0 | | 0 | 1 | 0 | 0 | | 2 | 0 | 0 | 0 | | 0 | 1 | 0 | 0 | |
0 | 0 | 1 | 0 | | 0 | 0 | 0 | 1 | | 0 | 0 | 2 | 0 | | 0 | 0 | 0 | 1 |
| |
|
⋅ | |
| |
| = | |
In either case, we can now approach the problem by finding the closest vector or matrix that is in the span of the matrix on the left-hand side of the equation.
We do this by finding the orthogonal projection of the right-hand side onto the span of the matrix.
The above tells us that it is sufficient to project the vector [2; 3; 4; 2] onto the span. The projection is:
| ( | | ⋅ | | ⋅ (1/√(3))) ⋅ | | ⋅ (1/√(3))
+ ( | | ⋅ | | ⋅ (1/√(2))) ⋅ | | ⋅ (1/√(2))
|
|
The above yields:
We can now set up an equation that has a solution:
| = | | | | | | 1 | 10/3 | | 0 | 5/2 | | 2 | 20/3 | | 0 | 5/2 |
| |
| |
| | ≈ | |
4.9. Application: distributed computation of least-squares approximations
Fact: We assume there are n distinct computing devices { C0, ..., Cn} (e.g., servers, virtual machines, motes, mobile devices, etc.), that
any device can communicate with a small number (e.g., two) of other devices at any given moment in time, and that all devices can compute or
communicate simultaneously (i.e., independently of one another). Then the following are true:
- if Ci knows some small piece of information (e.g., a real number r ∈ R), the devices can distribute r to all the devices in about log n time steps;
- if every device Ci has some real number ri, the devices can collectively compute r1 + ... + rn in about log n time steps.
Fact: The process of finding an approximate solution v* to an overdetermined system M ⋅ v = w can be broken down into the following basic operations:
- addition and subtraction of vectors;
- projection of one vector onto another vector;
- solving a system M ⋅ v* = w* that must have a solution.
Fact: If two vectors [a1; ...; an] and [b1; ...; bn] are stored in a distributed manner across multiple devices {C0, ..., Cn} such that device Ci stores only ai and bi, then the devices can collective compute the sum of these two vectors in one time step: each device Ci simply computes ai + bi
and stores the result internally.
4.10. Orthogonal complements and algebra of vector spaces
Definition: The orthogonal complement W⊥ of a vector subspace W ⊂ V is the set of all vectors in V that are orthogonal
to all the vectors in W:
W⊥ = {v | v ∈ V, ∀ w ∈ W, v ⋅ w = 0}
Notice that the orthogonal complement of a subspace is always taken within the context of some specified space V.
We consider vector spaces, their orthogonal complements, and common set operations: set union, set intersection, and set product.
Example: Given any two vectors spaces V and W, is V ∪ W a vector space? No. For example, consider
V = span{[1;0]} ∪ span{[0;1]}.
We have that [1;0] ∈ V and [0;1] ∈ V, but not [1;0] + [0;1] = [1;1] ∈ V.
Example: Given any two vectors spaces V and W, is V ∩ W a vector space? Yes.
- there is a unique additive identity: 0 ∈ V and 0 ∈ W, so 0 ∈ V ∩ W
- V ∩ W is closed under addition (+): if v,w ∈ V ∩ W then we have that v ∈ V and w ∈ V, and we also have that
v ∈ W and w ∈ W, so we have that
v + w ∈ V and v + w ∈ W, so v + w ∈ V ∩ W.
Since addition satisfies the vector space axioms for elements V and W, it also does so for elements in V ∩ W.
- V ∩ W is closed under scalar multiplication (⋅): if v ∈ V ∩ W then we have that v ∈ V and w ∈ V, so we have that
sv ∈ V and sv ∈ W, so sv ∈ V ∩ W.
Since scalar multiplication satisfies the vector space axioms for elements V and W, it also does so for elements in V ∩ W.
Example: Given any two vectors spaces V and W, is V × W a vector space? Yes.
Exercise: For a vector space W ⊂ V, compute W ∩ W⊥.
Fact: For a vector subspace W ⊂ V,
dim W + dim W⊥ = dim V.
Fact: For a vector subspace W ⊂ V,
W × W⊥ = V.
5. Linear Transformations
5.1. Set products, relations, and maps
We consider the following sets of vectors and their properties.
| construct |
definition |
example |
graphical example |
| V × W |
{ (v,w) | v ∈ V, w ∈ W } |
{1,2,3} × {4,5,6}
=
{(1,4),(1,5),(1,6),
(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6)} |
|
| R is a relation between V and W |
R ⊂ V × W |
{(1,D), (2,B), (2,C)}
is a relation between
{1,2,3,4} and {A,B,C,D} |
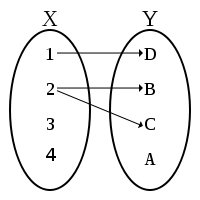 |
f is a function from V to W
f is a map from V to W |
f is a relation between V and W and
∀ v ∈ V, there is at most one
w ∈ W s.t. f relates v to w
|
{ (x,f(x)) | f(x) = x2 } |
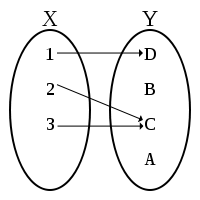 |
| R -1 is the inverse of R |
{ (w,v) | (v,w) ∈ R } |
|
|
| f: X → Y is injective |
|
|
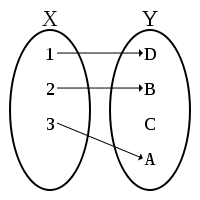 |
| f: X → Y is surjective |
|
|
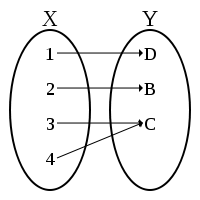 |
| f: X → Y is bijective |
|
|
 |
Notice that we may have f such that f is a function, but f -1 is not a function.
Fact: If we say that a map f is a relation between V and W, we can denote this as f : V → W or f ∈ V → W.
Then, V is the domain of f and W is the codomain.
Notice that the definition of f does not uniquely determine its codomain. For example,
f(x) = x2 could have a codomain of R if f : R → R, or it could have a codomain of R+ if f : R → R+.
Example: Describe with as much detail as you can the domains, codomains, and images of the following maps (there is more than one right
answer for these, as the definitions do not specify the domains of the functions). Determine whether each map is injective, surjective, or both
given the domains and codomains you chose.
| = | | | | | = | | | | | = | | | | | = | | | | | = | | | | | = | | | | where M and N are matrices
|
|
Fact: Given some f: V → W, the following process can be used to show a map f is injective:
- assume v,v' ∈ V and v ≠ v';
- it is necessary to show that f(v) ≠ f(v'):
- expand f(v) and f(v') using the definition of f;
- use algebraic properties or other facts to derive f(v) ≠ f(v').
Alternatively, we can use the following approach:
- assume v,v' ∈ V;
- assume f(v) = f(v'):
- expand f(v) and f(v') using the definition of f;
- use algebraic properties or other facts to derive v = v'.
Fact: Given some f: V → W, the following process can be used to determine whether a map f is surjective:
- let w ∈ W;
- solve f(v) = w:
- if you can solve the equation (or derive an equation v = g(w)) such that v ∈ V, f:V → W is surjective;
- if the equation has no solutions in V, f:V → W is not surjective.
Notice that the above does not mean that there is not some V' where V ⊂ V' that does have a solution
to the equation f(v) = w. For example, f(x) = 3 x is surjective if f ∈ R → R but not surjective
if f ∈ Z → Z.
Example: Show that f: R → R where f( x) = x + 1 is injective.
We can show this as follows by first adding 1 to both sides, then applying the definition of f:
Alternatively, we could use the other method by first apply the definition of f, then subtracting 1 from both sides.
Example: Show that f: R → R where f( x) = x + 1 is surjective.
Suppose any value in the codomain r ∈ R is chosen. Then we can solve the following equation for a corresponding value x in the domain:
Definition: A map f: V → W is a bijection or is bijective if f is an injection from V to W and f is a surjection from V to W.
Example: Show that f: R → R where f(x) = x + 1 is bijective.
Definition: Given a map f: V → W, we call { f( v) | v ∈ V } the image of f:
5.2. Homomorphisms and isomorphisms
The previous section defined a number of properties of functions f: A → B that only address the equality of elements in A and B. However,
what if A and B have relations and operators? For example, what if A and B are vector spaces with an identity, an addition operation, and a
scalar multiplication operation?
We can restrict our notion of a map or function to maps or functions f: A → B that somehow preserve or consistently transform the properties
of operators and relations we may have already defined on A and B. For example, suppose we have A = {a1, a2, a3}, B = {b1, b2, b3},
an operator ⊕ such that a1 ⊕ a2 = a3, and an operator ⊕ over elements of B such that b3 ⊕ b2 = b1. A map f from
A to B that preserves (or respects, or consistently transforms) ⊕ would be such that
Notice that the above map is such that the operation ⊕ is respected by the map f:
| f(a3) = f(a1 ⊕ a2) = f(a1) ⊕ f(a2) = b3 ⊕ b2 = b1 |
| |
Definition: Given a binary operator ⊗ over A and another operator ⊕ over B, we say that a map f: A → B is a homomorphism
if we have that
∀ a,a' ∈ A, f(a ⊗ a') = f(a) ⊕ f(a').
Notice that a homomorphism might have, but does not necesserily have, any of the properties we introduced for maps: it could be injective, surjective,
and so on.
Definition: A bijective homomorphism f: A → B is called an isomorphism.
5.3. Linear transformations
In this course we are interested in a specific kind of homomorphism.
Definition: For any two vector spaces V and W, a map f: V → W is a linear transformation iff we have that for all v, v' ∈ V and
scalars s ∈ R,
In other words, a linear transformation is a homomorphism between vector spaces that preserves vector addition and scalar multiplication.
If a map f does not satisfy the above properties, it is not a linear transformation.
Example: For any matrix M ∈ Rn×m, the map f : Rm → Rn defined as f( v) = M ⋅ v is a linear transformation.
We can confirm that any such f satisfies the properties of a linear transformation:
Example: Representation of a polynomial curve f as a vector of its y values on some fixed number of inputs x1,..., xn is a linear transformation.
Suppose we have the transformation φ defined as follows:
We can confirm that φ is a linear transformation. Suppose that h( x) = f( x) + g( x). Then we have:
| = | | | = | | | = | | | | | | f(x1) + g(x1) | | ⋮ | | f(xn) + g(xn) |
| |
| |
| | = | | | = | |
Suppose that h( x) = s ⋅ f( x). Then we have:
Fact: For any two linear transformations f: V → W, g: U → V, the composition f o g: U → W is also a linear transformation.
To show this, we must demonstrate that if h( x) = f( g( x)) then h respects vector addition and scalar multiplication. For any u, u' ∈ U, and
s ∈ R, we have:
and
Because linear transformations are homomorphisms (and, thus, maps), we can ask whether they have properties of maps (i.e., whether they are injective,
surjective, bijective, and so on). We will do so further below.
Example: Let the map φ : R3 → { f | f( x) = a x2 + b x + c} be defined as follows:
| = | | h where h(x) = a x2 + b x + c
|
|
It is the case that φ is a linear transformation and a bijection. Thus, φ is an isomorphism between R3 and
{ f | f( x) = a x2 + b x + c}.
Example: Differentiation (i.e., finding the derivative) of polynomials is a linear transformation.
As an example, consider the space of polynomials of the form f(x) = a x2 + b x + c. If each polynomial is represented as a vector
of its coefficients, the differentiation operator for this vector space of functions can be represented as a matrix:
Because there exists an isomorphism φ between { f | f( x) = a x2 + b x + c} and R3, we can compose φ and φ -1 with
the following linear transformation ψ : R3 → R3
Then, the following differential operator d/d x : { f | f( x) = a x2 + b x + c} → { f | f( x) = a x2 + b x + c} is a linear transformation because composition of linear transformations are linear transformations:
Example: Orthogonal projection onto a vector space is a linear transformation.
We know that any vector space has an orthonormal basis B. Thus, we can compute the projection of any vector v using the formula MB ⋅ MB⊤ ⋅ v.
Thus, orthogonal projection onto span B can be defined as a linear transformation f where:
Since ( MB ⋅ MB⊤) is a matrix, f must be a linear transformation.
Fact: For any linear transformation f: V → W and appropriate constants 0 ∈ V and 0' ∈ W,
f(0) = 0'
We can show this in the following way: given any v ∈ V,
Fact: For any linear transformation f: V → W and the corresponding additive inversion operations of
V and W, it is the case that f respects additive inversion:
f(-v) = -f(v)
We can derive this fact in two ways. One approach is to use the previous fact that f(0) = 0' to show that f(-v) is indeed the inverse of f(v):
The other approach is to use the fact that in both vector spaces,
v = -1 ⋅ v:
Then, because f respects scalar multiplication, we have that:
Thus, the argument is:
5.4. Orthogonal projections as linear transformations
Fact: For v ∈ Rn, an orthogonal projection onto a one-dimensional vector space span{ w} is a linear transformation. First,
note that the dot product of two vectors can be rewritten as matrix multiplication of two matrices:
w ⋅ v = w⊤ ⋅ v.
Also, notice that
Finally, notice that for nonzero r ∈ R where r ≠ 0, the 1 × 1 matrix | | ∈ R1 × 1 is invertible and has inverse | | .
Consider the formula for the projection of w ∈ Rn onto span(v). We can rewrite the formula to use only multiplication of matrices.
| = | | | = | | | = | | | = | | w ⋅ (w⊤ ⋅ w) -1 ⋅ (w⊤ ⋅ v) |
| | = | | (w ⋅ (w⊤ ⋅ w) -1 ⋅ w⊤) ⋅ v
|
|
Thus, we have a product of the matrices w ∈ Rn×1, (w⊤ ⋅ w) -1 ∈ R1×1, and w⊤ ∈ R1×n.
This product is a matrix in Rn×n. Call it Mspan{w}. Then we can define the linear transformation f ∈ Rn → Rn
that performs the orthogonal projection onto span{w} as:
f(v) = Mspan{w} ⋅ v.
We used the above approach because we will see later that it can be generalized to orthogonal projections onto multidimensional vector spaces.
An alternative way to show the above is to notice that w/||w|| can be rewritten as a matrix u ∈ Rn×1. In that case, we have:
Here, u ⋅ u⊤ ∈ Rn×n.
Example: Suppose we want to compute the projection of v onto w where:
We can compute the projection as follows:
| = | | | = | | ( | | ⋅ ( | | ⋅ (1/5))) ⋅ ( | | ⋅ (1/5)) |
| | = | | | = | | | = | | | = | | | = | | | = | | | = | |
Notice that the columns of the matrix above are in span { w}:
Thus, we have that:
Fact: Suppose that for M ∈ Rn×m and f ∈ Rm → Rn we have an overdetermined system:
M ⋅ v = w
If M⊤ ⋅ M is invertible (and, thus, (M⊤ ⋅ M) -1 is defined), we can say that:
| = | | | = | | | = | | |
(M⊤ ⋅ M) -1 ⋅ (M⊤ ⋅ M) ⋅ v | |
| = | | | = | | | = | |
Thus, even if M ⋅ v = w is overdetermined, M⊤ ⋅ ( M ⋅ v) = M⊤ ⋅ w has a solution v* such that M ⋅ v* corresponds
to the orthogonal projection of v onto the span of the column vectors of M.
Thus, for any matrix M where M⊤ ⋅ M is invertible, we can define the linear transformation that represents orthogonal projection onto
the span of the columns of M:
5.6. Matrices as linear transformations
Fact: Suppose we have the following matrix M ∈ Rm×n and the corresponding linear transformation f : Rn → Rm:
Then the following is true:
Fact: Suppose we have an invertible matrix M ∈ Rn×n and the corresponding linear transformation f : Rn → Rn:
Then f is a bijection. Because f is also a linear transformation, f is an isomorphism.
Example: Consider the following linear transformation f: R → R2:
The linear transformation f is injective but not surjective.
We can show f is injective:
To show it is not surjective, we choose the following vector w ∈ R2 (i.e., in the codomain). The equation is then not solvable,
so f is not surjective.
Example: Consider the following linear transformation f: R2 → span{ [3;4] }:
The linear transformation f is surjective but not injective.
Example: Consider the following linear transformation f: R2 → span{ [3;4] }:
The linear transformation f is surjective but not injective.
5.7. Application: communication
We want to transmit information, but we have constraints (e.g., security or high cost of transmission).
Suppose we have two linear transformations f : V → W and f -1 : W → V
such that f -1 o f is a bijection (and, thus, an isomorphism). If im(f) has some desirable property that the domain of f does not
possess (e.g., it is obscured, or it has a smaller representation size), we can use f as an encoding function for the information
we want to transmit, and f -1 as a decoding function.
Example: Suppose Alice wants to transmit the following vectors to Bob:
If she simply transmitted the individual real numbers to Bob one-by-one, she would need to transmit 10 real numbers.
Can Alice and Bob agree on some protocol that would allow Alice to send fewer real numbers but transmit the same amount of information in
this case?
All the vectors in the set are in R2. However, Alice and Bob can take advantage of the fact that the vectors are in a subspace of R2. In
particular, all five vectors are in:
Suppose Alice and Bob define the following encoding and decoding linear transformations:
Then f -1 o f is invertible, and Alice can use f to encode vectors that contain two real numbers within a single real number. This
means it is sufficient for Alice to send just five real numbers in order to send Bob the five vectors:
| { f( | | ), f( | | ), f( | | ), f( | | ), f( | | ) } | |
| = | |
5.8. Affine spaces and affine transformations
We are interested in studying solution spaces of systems of the form M ⋅ v = w. However, these are not vector spaces because they do not always contain 0 (i.e., the origin).
Recall that if a solution space of a system does contain 0, the solution space is a vector space and M ⋅ v = w must be a homogeneous system where w = 0.
Definition: Suppose W is a set of vectors such that 0 ∉ W, and suppose w0 is the orthogonal projection of 0 onto W. Then we can define
W to be a vector space with the following vector addition and scalar multiplication operations:
- addition (⊕) can be defined as follows. It is an operation on elements of W under which W is closed, and which satisfies the vector space axioms:
v ⊕ v' = u where u = (v - w0) + (v' - w0) + w0 = v + v' - 2 ⋅ w0 + w0 = v + v' - w0.
- scalar multiplication (⊗) can be defined as follows. It is an operation on elements of A under which A is closed,
and which satisfies the vector space axioms:
s ⊗ v = u where u = (s ⋅ (v - w0)) + w0 = s v - s w0 + w0 = s v + (1-s) ⋅ w0.
- there is a unique additive identity in W; it is the vector w0:
v ⊕ w0 = v + w0 - w0 = v.
Fact: If V is a vector space with addition operation + and scalar multiplication operation ⋅,
the vector space W = { v + w0 | v ∈ V} with addition operation ⊕ and scalar multiplication operation ⊗ is
isomorphic to V, with isomorphism f: V → W defined as:
We can see that f is a linear transformation because it has the properties of a linear transformation:
| = | | | = | | | = | | | = | | (v + w0) + (v' + w0) - w0 |
| | = | | | = | | | = | | s ⋅ v + w0 + (s ⋅ w0 - s ⋅ w0) |
| | = | | s ⋅ v + s ⋅ w0 + w0 - s ⋅ w0 |
| | = | | s ⋅ (v + w0) + (1-s) ⋅ w0 |
| | = | |
We can see it is injective:
We can see it is surjective because for any w' ∈ W:
Since f is injective, surjective, and a linear transformation, it is an isomorphism. Thus, V and W are isomorphic. This means we can work with W as if it is a vector space
by simply mapping back to V using the isomorphism, doing any necessary work, and then mapping back to W by using the inverse of that isomorphism, f -1.
Example: Consider the following affine space:
Suppose we want to find the orthogonal projection of the following point p ∈ R onto the affine space W:
To do so, we first need to find the isomorphism between a vector space V and the space W. We will choose the vector space V that is parallel to W but that goes through
the origin; it is defined as:
Notice that V is a line with the same slope as W. Next, we must the additive identity w0 of W by finding the intersection of V⊥ and W, where V⊥ is the orthogonal
complement of V. We first compute V⊥:
| = | | | = | | { u | u ⋅ v = 0 for all v ∈ V} |
| | = | | { u | u ⋅ v = 0 for all v ∈ basis V} |
| | = | | { u | u ⋅ v = 0 for all v ∈ { | | }} |
| | = | | | = | | | = | | | = | |
We can now compute the intersection and, thus, w0:
| = | | | = | | { | | | y = 2 x + 3} ∩ { | | | y = -(1/2) x } |
| | = | | { | | | y = 2 x + 3 and y = -(1/2) x} |
| | = | | | = | |
We can now define an isomorphism f: V → W:
Next, to project the point p onto W, it is now sufficient to first project the point onto V, then apply f:
| orthogonal projection of | | onto span { | | } | |
| = | | ( | | ⋅ (1/√(5)) | | ) ⋅ (1/√(5)) | | |
| | = | | | = | | | = | |
Finally, the orthogonal projection of p onto W can be computed via f:
| orthogonal projection of | | onto W | |
| = | | | = | | | = | |
How do we find an isomorphism between an affine space and a parallel vector space?
Fact: Suppose that for a matrix M ∈ Rn×n, M ⋅ u = w
is a non-homogeneous system with at least one solution. Let U be the solution space of M ⋅ u = w:
How can we find an isomorphism between U and some vector space V? We let V be the corresponding homogeneous system:
We must now find V⊥; we can do so by taking the transpose of M and setting up a new homogeneous system:
To find u0, it is now sufficient to find the intersection of U and V⊥:
The isomorphism f: V → U is then:
Example: Suppose we have a non-homogeneous system M ⋅ v = w where M ∈ Rn×n and we want to compute the projection of some p ∈ Rn onto the affine
space { v | M ⋅ v = w}. How can we do so?
Suppose that M is of the following form:
Then we can say that we want to project p onto { v | M ⋅ v = 0} and find an isomorphism f: { v | M ⋅ v = 0} → { v | M ⋅ v = w}; the
orthogonal projection is then f( p).
Thus, we find an orthonormal basis of {v | M ⋅ v = 0} and compute the orthogonal projection of p onto {v | M ⋅ v = 0}; call this p*:
| = | | orthogonal projection of p onto {v | M ⋅ v = 0}
|
|
We then find f by solving the following system of equations for u0:
We solve the above by first solving for v and then computing u0:
We now have the isomorphism f:
Then, we can compute the orthogonal projection:
| orthogonal projection of p onto {v | M ⋅ v = w} | |
| = | | = | |
Example: We can find a basis of the following set of solutions of a homogeneous system (thus, a vector space):
We can do so by starting with a basis that spans the entire space that contains V (which in this case is R2),
and then "removing" the contribution of the orthogonal complement V⊥ from these basis vectors.
Thus, we begin with:
We know that:
Thus, we project each basis vector for R2 onto V⊥, then subtract that from the basis vector:
| | | - ( | | ⋅ (1/√(5)) ⋅ | | ) ⋅ (1/√(5)) ⋅ | | | |
| = | | |
| | - ( | | ⋅ (1/√(5)) ⋅ | | ) ⋅ (1/√(5)) ⋅ | | | |
| = | |
The remaining vectors above span V:
5.9. Fixed points, eigenvectors, and eigenvalues
We introduce several properties of linear transformations; these properties it possible to work with linear transformations in new and convenient ways.
Definition: Given a linear transformation f: V → V, v ∈ V is a fixed point of f if:
Example: Consider the following linear transformation f: R2 → R2:
The following vector v is a fixed point of f:
Fact: For any linear transformation f, 0 is a fixed point of f (see the definition of a linear transformation).
Fact: If v is a fixed point of f and v ≠ 0, then f has an infinite number of fixed points. This is because for any s ∈ R and
any fixed point v, we have that:
Fact: For any linear transformation f where f( v) = M ⋅ v, let S be the set of fixed points of f:
S = {v | f(v) = v }
Then S is a vector space. There are several ways to show this. Let v be any fixed point of f. Then we have:
Thus, the fixed points of f represented by M are exactly the elements of the solution space of the homogeneous system (M - I) ⋅ v = 0.
Alternatively, we could show that S contains 0, S is closed under scalar addition, and S is closed under scalar multiplication.
We can generalize the notion of a fixed point by observing that a fixed point is just a vector on which the linear transformation acts
as a scalar multiplier (in the case of a fixed point, the multiplier is 1). If v is a fixed point of f, then we have that:
f(v) = 1 ⋅ v
What if we created another notion that was not restricted to 1?
Definition: Given a linear transformation f: V → V, v ∈ V is an eigenvector of f with eigenvalue
λ if:
f(v) = λ ⋅ v
Fact: For any linear transformation f, if v is a fixed point of f, then it is an eigenvector of f with eigenvalue 1.
Definition: The set of eigenvectors of a linear transformation f that have eigenvalue λ is its eigenspace:
| eigenspace of f with eigenvalue λ | |
| = | |
Any eigenspace is a vector space.
Fact: Given a linear transformation f ∈ Rn → Rn represented by M ∈ Rn×n and an eigenvector v, consider the following:
The above equation has only zero solutions if ( M - λ I) is invertible:
| = | | |
(M - λ I) -1 ⋅ (M - λ I) ⋅ v | |
| = | | | = | | | = | |
Thus, nonzero eigenvectors v exist only if ( M - λ I) is not invertible. However, if it is not invertible, this means that det ( M − λ I) = 0. Thus, if it
is the case that det ( M - λ I) = 0, then there must exist at least one λ that solves this equation. In fact, the eigenvalues
of T are exactly the solutions to the equation:
Example: Suppose that we are modelling a system with two dimensions that are each modelled using R:
- population in the city;
- population in the suburbs.
The following matrix (call it T) represents the movement of the two populations between the two locations (with entries in percentages) over
one year:
|
|
from city |
from suburbs |
|
| to city |
|
0.95 stay in the city |
0.03 move from suburbs to city |
|
| to suburbs |
|
0.05 move from city to suburbs |
0.97 stay in the suburbs |
|
For example, suppose the population in 1999 is represented by v below. Then the population in 2000 is represented by T ⋅ v:
Let f(v) = T ⋅ v be the linear transformation represented by T.
- What does a fixed point of f represent?
A fixed point of f represents a stable population distribution that will not change from one year to the next. For example:
Notice that any scalar multiple of this vector, including a vector that is normalized so that the two components add up to 1,
is also a fixed point of f:
Thus, for this transformation, for any distribution of the population in which 37.5% live in the city, the distribution is stable.
- What does an eigenvector of f represent?
An eigenvector of f represents a population distribution that may grow or shrink, but whose relative distribution between the city and
the suburbs remains the same from one year to the next.
-
Does f have any nonzero eigenvectors other than the fixed points?
No, because the sum of the components of any vector in im f is always the same as the sum of the components of the input vector that produced
that image.
| = | | | | | | 0.95 x + 0.03 y | | 0.05 x + 0.97 y |
| |
| |
| | = | | (0.95 x + 0.05 x) + (0.03 y + 0.97 y) |
| | = | | (0.95 x + 0.03 y) + (0.05 x + 0.97 y)
|
|
This is because the sums of the components of the column vectors of T are 1. This makes T a stochastic matrix, and it makes
the fixed points the steady-state or equilibrium vectors of T.
-
Find the vector space of fixed points of f.
Note that either the fixed points of f are {0}, or there are infinitely many. Thus, if we can find a matrix equation whose solutions
are the fixed points, we will obtain either a system whose only solution is 0, or an underdetermined system.
We know that for our particular f and T, the space of fixed points is the set of solutions to the equation:
We then find the basis that spans S:
-
Suppose we want to find a closed formula for the population k years after the initial state v (i.e., after applying T to an initial
vector v eight times, or Tk ⋅ v) where we have:
The formula should be in terms of k and should not require matrix multiplication. In other words,
we should be able to obtain closed formulas for the city population and the suburb population in terms of k.
We can approach this problem by finding the eigenvectors of f. Then, we can express the result of Tk ⋅ v
as a linear combination of eigenvectors.
| = | | |
det | | | | 0.95 - λ | 0.03 | | 0.05 | 0.97 - λ |
| |
| | |
| = | | |
(0.95 - λ) ⋅ (0.97 - λ) - (0.03 ⋅ 0.05) | |
| = | | |
λ2 - 1.92 λ + 0.9215 - 0.0015 | |
| = | | | = | | | = | | (1.92 ± √(1.922 - 4(0.92)))/2 |
| | = | | | = | | | = | |
We already know the eigenvector for eigenvalue 1 (it is the fixed point). To find the eigenvector for the other eigenvalue, we solve:
Thus, our eigenvectors are:
Notice that we had a space of solutions because the system was underdetermined; we chose a particular eigenvector. Finally, notice that:
| = | | (Tk ⋅ a ⋅ e1) + (Tk ⋅ b ⋅ e2) |
| | = | | a ⋅ (Tk ⋅ e1) + b ⋅ (Tk ⋅ e2) |
| | = | |
Thus, if the initial input vector can be rewritten in terms of the two eigenvectors, we can find the closed formula. In fact, it can be
because the two eigenvectors are linearly independent:
The closed formula is:
| = | | 0.125 ⋅ | | + 0.225 ⋅ 0.92k ⋅ | |
|
|
Eigenspaces have many other applications. In particular, they make it possible to provide "natural" interpretations of general notions of
concepts such as differentiation in the context of vector spaces.
Example: Differentiation is a linear transformation from the vector space of differentiable functions (or a subset, e.g., the polynomials):
As an example, consider the space of polynomials of the form f(x) = a x2 + b x + c. If each polynomial is represented as a vector
of its coefficients, the differentiation operator for this vector space of functions can be represented as a matrix:
Thus, an eigenvector in this vector space is any differentiable function f such that:
Notice that the above is a differential equation. If λ = 0, then we have for any constant c ∈ R the solution:
If λ ≠ 0 and we do not restrict ourselves to polynomials but allow all infinitely differentiable functions, then we have the solution:
Review 2. Vector and Matrix Algebra, Vector Spaces, and Linear Transformations
The following is a breakdown of what you should be able to do at the end of the course
(and of what you may be tested on in an exam).
Notice that many of the tasks below can be composed.
This also means that many problems can be solved in more than one way.
- vectors
- definitions and algebraic properties of scalar and vector operations (addition, multiplication, etc.)
- vector properties and relationships between vectors
- dot product of two vectors
- norm of a vector
- unit vectors
- orthogonal projection of a vector onto another vector
- orthogonal vectors
- linear dependence of two vectors
- linear independence of two vectors
- linear combinations of vectors
- linear independence of three vectors
- lines and planes
- line defined by a vector and the origin ([0; 0])
- line defined by two vectors
- line in R2 defined by a vector orthogonal to that line
- plane in R3 defined by a vector orthogonal to that plane
- matrices
- algebraic properties of scalar and matrix multiplication and matrix addition
- collections of matrices and their properties (e.g., invertibility, closure)
- identity matrix
- elementary matrices
- scalar matrices
- diagonal matrices
- upper and lower triangular matrices
- matrices in reduced row echcelon form
- determinant of a matrix in R2×2
- inverse of a matrix and invertible matrices
- other matrix operations and properties
- determine whether a matrix is invertible
- using the determinant for matrices in R2×2
- using facts about rref for matrices in Rn×n
- algebraic properties of matrix inverses with respect to matrix multiplication
- transpose of a matrix
- algebraic properties of transposed matrices with respect to matrix addition, multiplication, and inversion
- matrix rank
- matrices in applications
- solve an equation of the form LU = w
- matrices and systems of states
- interpret partial observations of system states as vectors
- interpret relationships betweem dimensions in a system of states as a matrix
- given a partial description of a system state and a matrix of relationships, find the full description of the system state
- interpret system state transitions/transformations over time as matrices
- population growth/distributions over time
- compute the system state after a specifieds amount of time
- find the fixed point of a transition matrix
- vector spaces
- vector spaces and their properties
- given a set of vectors or other objects, show that it is a vector space
- express a vector space as a span of a finite set of vectors
- given two vector spaces defined using span notation, show one is a subspace of the other
- given two vector spaces defined using span notation, show they are equal
- find the basis of a vector space
- find an orthonormal basis of a vector space
- find the dimension of a vector space
- find the orthogonal complement of a vector space
- particular vector spaces
- the set of polynomials {f | f(x) = ak xk + ... + a1 x + a0, a1,...,ak ∈ R}
- the solution set of an equation { v | M ⋅ v = w }
- affine spaces
- find the least-squares approximation of an overdetermined linear system
- linear transformations
- determine if a relation is a map
- determine if a map is a linear transformation
- given a linear transformation (and/or its matrix representation)...
- show it is injective
- show it is surjective
- show it is bijective
- find its image (a vector space)
- find its space of fixed points
- find its eigenvalues
- find its eigenvector for a given eigenvalue
- compositions of linear transformations and their properties
- compute orthogonal projections...
- onto the span of a single vector in Rn
- onto a subspace of Rn...
- by first computing an orthonormal basis and then using it to find the projection
- by using the formula M ⋅ M⊤ if M has orthonormal columns
- by using the formula M ⋅ (M⊤ ⋅ M) -1 ⋅ M⊤
- applications and solving systems of equations
- curve fitting
- find a polynomial curve that exactly fits a given set of points in R2
- find a least-squares approximate polynomial curve that best fits a set of points in R2
Below is a comprehensive collection of review problems going over the material covered in this course. These problems are an
accurate representation of the kinds of problems you may see on an exam.
Example: Consider the following vector space:
- Find the orthogonal projection of the following vector onto V:
If the two spanning vectors were orthogonal, one approach would be to project u onto a normalized
form of each vector, and to add the results. If the two spanning vectors were orthonormal, it would be
sufficient to simply project onto each vector, and add the results. Because the two vectors are neither,
we can use the formula M (M⊤ M) -1 M⊤ u for the projection where
- Find a basis of V⊥.
It is sufficient to set up an underdetermined
system, solve for two of the variables in terms of the third, and set the third to an arbitrary constant:
| = | | | = | | | = | | | = | | -y/2 - 4z/2 = -z/2 - 4z/2 = -5/2 ⋅ z
|
|
Setting z = 2, we get:
- Find any matrix M such that for f(v) = M ⋅ v, f(v) = 0 for all v ∈ V.
It is sufficient to find a matrix that maps both spanning vectors to 0.
From above, we already have a vector that spans V⊥, so such a matrix can be computed using the formula:
Example: Consider the vector space of polynomials of degree at most 2:
F = { f | f(x) = a x2 + b x + c, a,b,c ∈ R}
The map d:F → F represent differentiation. For example:
- Determine whether d:F → F is injective.
It is not injective because we can find two unequal inputs that produce the same output. Consider the following polynomials:
Then we have that:
Thus, the map d is not injective.
- Recall that a polynomial can be represented as a vector. For example, f(x) = 5 x2 - 2 x + 3 can be
represented as:
Show that d is a linear transformation by finding a matrix representation for d.
The matrix representation is:
Notice that:
- Show that d:F → F is not surjective.
Intuitively, we see that there are only two linearly independent columns in the matrix representing d,
so there must be vectors in the codomain of d that are not in the image of d, so d is not surjective.
To prove this, we find some vector w in the codomain for which there is no solution to the following equation:
Since we derive a contradiction, the above equation must have no solution.
Example: Alice wants to send vectors in R2 to Bob. For any vector v ∈ R2 that
she wants to send, she generates a random scalar r ∈ R and sends w
to Bob as defined below:
- Find a matrix D ∈ R3× 3 that Bob can use to decode Alice's messages.
Alice is sending vectors that are a linear combination of two vectors that carry the two scalars in a message vector v and a noise vector:
Bob must first cancel out the noise using a matrix in R3. Then he must take the result of that and recover
the scalars x and y.
To find an appropriate matrix to cancel out the noise, Bob can use the following formula:
Once Bob applies C to the vector he receives from Alice, he has:
Notice that we can find a matrix that inverts this operation by replacing the top-left portion of the above encoding matrix with its inverse:
Thus, Bob can use the following matrix to decode messages:
If Bob receives a message w that is the encoded version of v, he can retrieve it by computing:
- Find a matrix D' ∈ R2×3 that Bob can use to retrieve v ∈ R2 given a transmitted w ∈ R3.
Bob simply needs to drop the third component of the result of D ⋅ C ⋅ w. This can be accomplished by computing:
Thus, an appropriate matrix in R2×3 would be:
Example: Suppose there are two locations across which a population is distributed. Over the course of each year,
the population moves between the two locations according to one of two population distribution transformations depending
on how well the economy is doing ( A if the economy is doing well, B otherwise):
- Find an initial state v ∈ R2 such that if the economy is always doing well,
the population distribution will remain the same.
We need to find a fixed point of f(v) = A ⋅ v. Since dim R2 = 2, we know that there are three possibilities:
- 0 is the only fixed point;
- the space of fixed points has dimension 1, so there are infinitely many fixed points that all fall on a single line;
- all points in R2 are fixed points.
We solve the following system:
Since one equation can be derived from the other, the above system is underdetermined, but x can be expressed in terms of y. Thus, the space
of fixed points is one-dimensional. Setting y = 10, it can be expessed as a span of the following fixed point vector:
- Suppose that over the course of several years, the economy has both done well and not well.
Has the total population (the sum of the populations in the two locations) changed over this
duration?
Notice that neither A nor B change the total population in the two locations as represented by a state vector in R2. Thus, the total
population has not changed.
Example: Given u ∈ Rn, what is the orthogonal projection of v ∈ Rn onto span{ u}?
It is sufficient to compute the orthogonal projection of v onto u. Given a unit vector e parallel to u, the projection of v onto e would
be:
(e ⋅ v) ⋅ e.
However, we cannot assume u is a unit vector. Thus, we scale u to obtain a unit vector e = u/||u||. Then, the solution is:
((u/||u||) ⋅ v) ⋅ (u/||u||).
Example: Let M ∈ R17× 9 and f( v) = M ⋅ v. What is the largest possible value of dim(im( f))?
We know that we can only compute M v if v has as many rows as M has columns. Thus, if f(v) = M ⋅ v, then v ∈ R9. We
also know that M ⋅ v will be a vector with 17 rows because M has 17 rows, so f(v) ∈ R17. Thus, f ∈ R9 → R17.
This means that dim(im(f)) cannot be greater than dim(R17), so it cannot exceed 17. However, we also need to note that M
has 9 columns, and that any value in the image of f is thus a linear combination of at most 9 vectors. Thus, any basis of im(f) has
at most 9 distinct vectors in it. Since dim(im(f)) is the size of the basis of im(f), dim(im(f)) can be at most 9.
Example: Find an orthonormal basis for the following vector space:
We can use the algorithm for computing the vectors in an orthonormal basis. We can work with the vectors in any order, so suppose we have:
According to the algorithm, we then let u1 = v1 and e1 = u1 / ||u1||. In this case, we still have e1 = v1. Next, we compute:
| = | | v3 - ((v3 ⋅ e1) ⋅ e1) - ((v3 ⋅ e2) ⋅ e2)
| |
| = | | = | | | | = | |
Thus, {e1, e2, e3} is an orthonormal basis for span{v1, v2, v3}.
Example: Suppose we are given a linear transformation f: R2 → R2 where:
- Find an orthonormal basis for im(f).
We know that the column vectors of the matrix are linearly independent. Thus, dim(im(f)) as at least 2, and since
the codomain of f is R2, im(f) = R2. Thus, any orthonormal basis of R2 is appropriate, such as:
- Find the set of all v such that f(v) = 0.
Let the matrix in the definition of f be M.
We know from lecture that M is invertible iff M ⋅ v = 0 has exactly one solution 0. Since det M ≠ 0, M is invertible, so
there is exactly one solution in the solution space {0}.
Alternatively, it is sufficient to find the set of solutions to the equation f(v) = 0, which is the set of solutions (expanding the
definition of f) of:
Since M is invertible, we can multiply both sides by M -1 to obtain:
Thus, there is only one solution in the solution set: {0}.
- Show that f is surjective.
To show that f is surjective, it is sufficient to show that for every v in the codomain, there exists x such that:
In other words, we want a formula for x in terms of v that is defined for any v. Let the matrix in the definition of f be M. Since M
is invertible, we can define:
This formula for x is always defined, so f is surjective.
Example: Suppose we are given a linear transformation f: R2 → R2 where:
- Find dim(im(f)).
Recall that the dimension of a space is the size of any basis of that space (all bases of a space have the same size). Let M be the
matrix in the definition of f. The space im(f) is equivalent to the span of the column vectors of the matrix:
To find a basis of a space spanned by a collection of vectors, we create a matrix whose rows are the vectors in that collection, find its
reduced row echelon form, and keep only the nonzero rows in the basis:
Thus, the dimension of im(f) is 1.
- Show that f is not injective.
To show that a map is not injective, it is sufficient to find v and v' such that v ≠ v' but f(v) = f(v').
One approach to finding such v and v' is to expand f(v) = f(v') until the constraints are simple enough that
it is straightforward to try some inputs and easily check that they satisfy the constraints.
Since the top row of the matrix is a multiple of the bottom row, we get one equation:
One possible pair of vectors in the domain that satisfies the above is:
Thus, f is not injective.
- Define the solution space f(v) = 0 as a span and find its basis.
We write down the definition of the solution space of the homogeneous system above:
The constraints imposed above can be summarized as:
Thus, the solution space is the line in R2 defined by the equation y = -2x. We can choose any vector on this line and take the span of the set
containing only that vector to provide an explicit definition for the set of solutions:
Example: Find a matrix M such that for f( v) = M ⋅ v,
One way to approach this problem is to expand the definition on the right-hand side using the
definition of the orthogonal complement operation:
| = | | { | | | 2x = 0, 2z = 0, y,t ∈ R } |
| | = | | { | | | x = 0, z = 0, y,t ∈ R } |
| | = | |
Thus,
Recall that the image of f is the span of the columns of M. Thus, one possible solution is:
Example: Suppose that a2 + b2 = 1. What is the orthogonal projection of v onto im( f) if f( v) = M ⋅ v, and:
We have that:
Because a2 + b2 = 1, the first vector is already a unit vector and orthogonal to the second vector. By rescaling the second vector to be
a unit vector, we can obtain an orthonormal basis:
We can now find the orthogonal projection of v onto each vector in the orthonormal basis, and add these to find the orthogonal projection of the
vector onto im( f):
Example: Suppose we are given the following points:
- Find a function of the form f(x) = ax2 + bx + c that is the best least-squares fit for these points.
We begin by writing down the equations in terms of f for each point:
We construct the matrix equation that represents the above system:
| | | | | (0)2 | (0) | 1 | | (2)2 | (2) | 1 | | (2)2 | (2) | 1 |
| |
| ⋅ | | | |
| = | |
There is no solution to the above equation. However, we are looking for the least-squares best fit approximation. Thus, we first find an
orthonormal basis of the image of the matrix. If the matrix is M and f(v) = M ⋅ v, we have that:
Using the algorithm for finding an orthonormal basis, we obtain:
|
We now find the orthogonal projection of | | onto im(f) and use it to rewrite the equation so that it is not overdetermined:
|
| | | | | (0)2 | (0) | 1 | | (2)2 | (2) | 1 | | (2)2 | (2) | 1 |
| |
| ⋅ | | | |
| = | |
This system is underdetermined. The space of solutions implied by the above equation is:
| { f | f(x) = ax2 + bx + c, c = 6, 4a + 2b + c = 9}
|
|
This means that any solution to the system is a least-squares best fit approximation. One possible best fit approximation is:
f(x) = x2 + (-1/2)x + 6
- Find a function of the form f(x) = bx + c that is the best least-squares fit for these points.
We follow the same process as in part (a) above. The matrix equation is:
There is no solution to the above equation. However, we are looking for the least-squares best fit approximation. Thus, we first find an
orthonormal basis of the image of the matrix. If the matrix is M and f(v) = M ⋅ v, we have that:
Using the algorithm for finding an orthonormal basis, we obtain:
|
We again find the orthogonal projection of | | onto im(f) and use it to rewrite the equation so that it is not overdetermined:
|
This yields c = 6 and b = 3/2. Thus, the least-squares best fit approximation is:
f(x) = (3/2)x + 6
Example: Show that for M ∈ Rn×n, the space of solutions to M x = 0 is a vector space (you do not need to show that
all the axioms hold; it is sufficient to show the appropriate closure properties).
Let S be the space of solutions.
We show that 0 ∈ S:
We show that if v,v' ∈ S, then v + v' ∈ S:
We show that if v ∈ S, then for any scalar s ∈ R, s v ∈ S:
Example: Compute the orthogonal projection of v onto im( f) where f( v) = M ⋅ v,
Normally, the way to approach such problems is to find an orthonormal basis for im(f) where f(v) = M ⋅ v, then use
that orthonormal basis to project v onto im(f). However, it's a good idea to check for special cases before delving into a large
computation. In this particular example, we have that:
Thus, v is orthogonal to both vectors, so the orthogonal projection of v onto im(f) is 0 ∈ R3.
It is worth noting that v is in the orthogonal complement of im(f). In general, given a vector subspace W ⊂ V,
for any w ∈ W⊥, the orthogonal projection of w onto W is 0.
Example: Is the system below overdetermined or underdetermined? Does it have a solution?
The system is neither overdetermined nor underdetermined. It has a solution. Since the matrix is upper triangular, we can use the
algorithm for solving a system with an upper triangular matrix to obtain v:
Example: Determine whether the system below has a solution for all possible v ∈ R3. If it does not, describe exactly
the set of vectors v for which the system below has a solution and determine whether this set a vector space.
Notice that determining whether the system has a solution for any v is equivalent to determining whether the linear
transformation represented by the matrix is surjective. It is also equivalent to determining whether the matrix is invertible.
To determine whether the matrix is invertible, we could compute its reduced row echelon form by finding an appropriate series of row operations.
Given the above, we see that the matrix is not invertible.
Let the matrix be M. The set of vectors for which there is a solution to the above equation is im(f) where f(x) = M ⋅ x. Thus,
we want to find im(f) explicitly. We could say:
If we want to be more precise, we could compute rref( M⊤) to find a basis for im( f).
Since the set of possible vectors v for which the equation has a solution is im(f) and f is a linear transformation, the set of such v is a vector
space.
| 



