- Introduction
- Vectors
- Defining operations on vectors
- Vector spaces
- Assignment #1: Vector Algebra
- Common vector properties, relationships, and operators
- Review of Notation: Logical formulas with quantifiers, sets, and set comprehensions.
- Review: Problems with Vector Algebra
- Applying Vectors and Linear Combinations to Problems
- Matrices
- Matrices and multiplication of a vector by a matrix
- Interpreting matrices as tables of relationships and transformations of system states
- Interpreting multiplication of matrices as composition of system state transformations
- Assignment #2: Matrix Algebra
- Matrix operations and their interpretations
- Matrix properties
- Solving the equation M v = w for M with various properties
- Row echelon form and reduced row echelon form
- Matrix transpose
- Orthogonal matrices
- Matrix rank
- Matrix similarity
- Review #1
- Vector Spaces
- Sets of vectors and their notation
- Equality of sets of vectors and vector spaces
- Vector spaces as abstract structures
- Subspace relation on vector spaces
- Finding a basis and an orthonormal basis of a vector space
- Assignment #3: Vector Spaces
- Homogenous, non-homogenous, overdetermined, and underdetermined systems
- Application: approximating overdetermined systems
- Application: approximating a model of system state relationships
- The dimension of a vector space
- Orthogonal complements of vector spaces
- Algebra of vector spaces
- Linear Transformations
- Maps (a.k.a., functions) and their properties
- Homomorphisms and isomorphisms
- Linear transformations
- Data modelling as a linear transformation
- Kernels of linear transformations
- Matrices as symbolic representations of linear transformations
- Assignment #4: Algebra of Linear Transformations
- Orthogonal Projections are Linear Transformations
- Review #2
- Applications to Linear Systems
- Review #3
- Appendix
Introduction
When real-world problems are addressed mathematically, the details of those problems are abstracted away until they can be represented directly as idealized mathematical objects (e.g., numbers, geometric structures, and so on). In this course, we will study one collection of such idealized mathematical objects: points, lines, planes, spaces, and the relationships and transformations between them that preserve linearity, (i.e. the straight characteristic of lines). This particular collection of "linear" objects and relationships can be used to represent many common real-world problems (and their possible solutions).
In order to study these objects and their relationships, we will define a symbolic language for naming them. We will define rules for this symbolic language (i.e., a linear algebra) and we will show that these rules correspond to the actual geometric properties of the objects that the language allows us to describe. We will then practice using this language to solve problems.
In this course, we will focus on problems that involve some number of degrees of freedom, each of which can be represented as a linear dimension (i.e., the real numbers). Each of these problems can typically be represented as a system of linear equations. The simplest examples of such problems should be familiar to most college students. Below is an example.
Example: Suppose we have $12,000 and two investment opportunities: one has an annual return of 10%, and the other has an annual return of 20%. How much should we invest in each opportunity to get $1800 over one year?
The above problem can be represented as a system of equations with two variables (each of which ranges over the real numbers):
| = |
| |||
| = |
|
The possible solutions to this system are the collection of all pairs of real numbers that can be assigned to (x,y). Notice that these can be interpreted directly as points on a plane.
Vectors
We will call points in geometric spaces vectors. We first define a notation for names of vectors. Vectors will be written using any of the the following equivalent notations (there are distinctions between these that will become relevant later).
Defining operations on vectors
We will also use symbols to name some geometric manipulations of vectors. One such operation is addition. Suppose we treat vectors as paths from (0,0), so that (2,3) is the path from (0,0) to (2,3) and (1,2) is the path from (0,0) to (1,2). Then vector addition would represent the final destination if someone walks first along the length and direction specified by one vector, and then from that destination along the length and direction specified by the other. The following definition for the operation + and vectors of two components corresponds to this intuition.
| = |
|
Notice that we have defined an entirely new operation; we are merely reusing (or "overloading") the + symbol to represent this operation. We cannot assume that this operation has any of the properties we normally associate with addition of real numbers. However, we do know that according to our interpretion of vector addition (walking along one vector, then along the other from that destination), this operation should be commutative. Does our symbolic definition conform to this interpretation? If it does, then we should be able to show that [x;y] + [x';y'] and [x+x';y+y'] are names for the same vector. Using the commutativity of the real numbers and our definition above, we can indeed write the proof of this property.
| = |
| ||||||||||||||||||||||||
| = |
| |||||||||||||||||||||||||
| = |
|
Recall that we can view multiplication by a number as repeated addition. Thus, we could use this intuition and our new notion of vector addition defined above to define multiplication by a real number; in this context, it will be called a scalar, and the operation is known as scalar multiplication.
|
Scalar multiplication has some of the intuitive algebraic properties that are familiar to us from our experience with R. Below, we provide proofs of a few.
| = |
| |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
# alternatively, we could also derive...
| = |
| |||||||||||||||||
| = |
|
Vector spaces
In this course, we will study collections of vectors that have particular properties. When a collection of vectors satisfies these properties, we will call it a vector space. We list these eight properties (in the form of equations) below. These must hold for any u, v, and w in the collection, and 0 must also be a vector in the collection.
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
|
Note that these are not unique; we could have specified an alternative equation for the additive identity.
Each equation can be derived from the other using the commutativity
These eight equations can be called axioms (i.e., assumptions) when we are studying vector spaces without thinking about the internal representation of vectors. For example, the above derivation of the alternative additive identity equation is based entirely on the axioms and will work for any vector space. However, to show that some other structure, such as R2, is a vector space we must prove that these properties are satisfied. Thus, to define a new vector space, we usually must:
- define a way to construct vectors;
- define a vector addition operator + (i.e., how to add vectors that we have constructed);
- specify the vector that is the additive identity (call it 0);
- define vector inversion: a process for constructing the inverse of a vector;
- prove that the eight properties of a vector space are satisfied by the vectors, +,0, and *.
Assignment #1: Vector Algebra
In this assignment you will perform step-by-step algebraic manipulations involving vectors and vector operations. In doing so, you will assemble machine-verifiable proofs of algebraic facts. Please submit your solutions by email in a single text file.
Working with machine verification can be frustrating; minute operations that are normally implied must often be explicit. However, the process should familiarize you with common practices of rigorous formal reasoning in mathematics: finding, applying, or expanding definitions to reach a particular formula that represents a desired argument or solution.
-
- Finish the proof below by solving for a using a sequence of permitted algebraic manipulations.
∀ a, b ∈ R,
a 4 = b + 3 b
implies
# put proof steps here
a = \undefined # should be an integer
- Finish the proof below by solving for b in terms of a.
∀ a,b ∈ R,
11 24 = 3 7 a + 1 2 b
implies
# ???
b = \undefined # should be an expression with "a"
- Finish the proof below to show that [1;2] and [-2;1] are linearly independent.
1 2 ⋅ -2 1 = 1 ⋅ -2 + 2 ⋅ 1 and
# ???( 1 2 ) and ( -2 1 ) are orthogonal - Solve for x (the solution is an integer).
∀ x ∈ R,
( x 4 ) and ( 1 1 ) are orthogonal
implies
# ???
x = \undefined
- Show that no [x; y] exists satisfying both of the below properties by deriving a contradiction (e.g.,
1 = 0).∀ x,y ∈ R,
( x y ) is a unit vector and ( x⋅x y⋅y ) and ( 1 1 ) are orthogonal
implies
# ???
\undefined # this should be a contradiction
- Finish the proof below by solving for a using a sequence of permitted algebraic manipulations.
- We have shown in lecture that R2, together with vector addition and scalar multiplication, satisfies some of the vector space axioms.
In this problem, you will show that the remaining axioms are satisfied.
- Finish the proof below showing that [0; 0] is a left identity for addition of vectors in R2.
∀ x,y ∈ R,
# ???
0 0 + x y = x y
- Finish the proof below showing that [0; 0] is a right identity for addition of vectors in R2.
∀ x,y ∈ R,
# ???
x y + 0 0 = x y
- Finish the proof below showing that 1 is the identity for scalar multiplication of vectors in R2.
∀ x,y ∈ R,
# ???
1 ⋅ x y = x y
- Finish the proof below showing that the component-wise definition of inversion is consistent with the inversion axiom for vector spaces.
∀ x,y ∈ R,
# ???
x y + (- x y ) = 0 0
- Finish the proof below showing that the addition of vectors in R2 is associative.
∀ a,b,c,d,e,f ∈ R,
# ???
a b + ( c d + e f ) = ( a b + c d ) + e f
- Finish the proof below showing that the distributive property applies to vector addition and scalar multiplication for R2.
∀ s, x, y, x', y' ∈ R,
# ???
s ( x y + x' y' ) = (s x y ) + (s x' y' )
- Finish the proof below showing that [0; 0] is a left identity for addition of vectors in R2.
-
Any point p on the line between vectors u and v can be expressed as a(u-v)+u for some scalar a. In fact, it can also be expressed as b(u-v)+v for some other scalar b. In this problem, you will prove this fact for R3.
Given some p = a(u-v)+u, find a formula for b in terms of a so that p = b(u-v)+v. Add this formula to the beginning of the proof (after
a =) and then complete the proof.∀ a,b ∈ R, ∀ u,v,p ∈ R3,
p = a(u-v) + u and a = \undefined # define a in terms of b
implies
# ???
p = b (u-v) + v
The verifier's library contains a variety of derived algebraic properties for R and R3 in addition to the vector space axioms for R3. Look over them to see which might be useful.
Common vector properties, relationships, and operators
We introduce two new operations on vectors (e.g. u and v): the norm (|| v ||) and the dot product (u ⋅ v). When interpreting some other structure, such as R2, as a vector space, we must provide definitions for these operators in order to use them.
| = |
| |||
| = |
|
Notice that the dot product is a new, distinct form of multiplication (distinct from multiplication of real numbers, and distinct from scalar multiplication). Also notice that the two operations are related:
These operations can be shown to have various algebraic properties. For example, the dot product is commutative.
| = |
| |||||||||||||||||
| = |
| ||||||||||||||||||
| = |
|
We also introduce several vector properties. Some deal with a single vector; some deal with two vectors; and some deal with three vectors.
The table below summarizes the vector properties and relationships and how they are related in some cases to vector operators and associated algebraic properties.
| property | definition | algebraic properties for R2 u = [x;y], v = [x',y'], w = [x'',y''] |
| v has length s | ||v|| = s or √(v ⋅ v) = s |
||v|| = √(x*x + x*y) = √([x,y] ⋅ [x,y]) |
| v is a unit vector | ||v|| = 1 or v ⋅ v = 1 |
1 = ||v|| = √(x*x + x*y) = √([x,y] ⋅ [x,y]) 1 = ||v|| = x*x + x*y = [x,y] ⋅ [x,y] |
| u and v are linearly dependent u and v are collinear |
∃ a ∈ R, a u = v | y/x = y'/x' |
| u and v are linearly independent | ∀ a ∈ R, a u ≠ v | y/x ≠ y'/x' |
| u and v are orthogonal | u ⋅ v = 0 | y/x = -x'/y' |
| w is a projection of u onto v | w = v ⋅ ((u ⋅ v)/||v||) | |
| w is a linear combination of u and v | ∃ a,b ∈ R, w = au + bv |
In R2, we can derive the linear independence of [x;y] and [x';y'] from the orthogonality of [x;y] and [x';y'] using a proof by contradiction. Consider the following.
| = |
| |||
| = |
|
Now, suppose that [x;y] and [x';y'] are not linearly independent. Then they are linearly dependent, so y/x = y'/x'. But this means that:
| = |
| |||
| = |
| |||
| = |
|
No real numbers y and x satisfy the above equation, so we must have introduced a contradiction by supposing that [x;y] and [x';y'] are not linearly independent. Thus, they must be linearly independent.
Some properties and operators of sets of vectors
Properties that can hold between two vectors (e.g. orthogonality) can often be generalized to sets of vectors. One way to do so is to require that for every pair of vectors in a set, the property holds.
| property | definition |
| {w1, ..., wn} are pairwise linearly dependent | ∀ u,v ∈ {w1, ..., wn}, u and v are linearly dependent |
| {w1, ..., wn} are pairwise linearly independent | ∀ u,v ∈ {w1, ..., wn}, u and v are linearly independent |
| {w1, ..., wn} are pairwise orthogonal | ∀ u,v ∈ {w1, ..., wn}, u and v are orthogonal |
| {w1, ..., wn, ...} are linear combinations of u and v {w1, ..., wn, ...} are linear combinations of u and v {w1, ..., wn, ...} is the span of u and v span{u,v} = {w1, ..., wn, ...} |
{ w | ∃ a,b ∈ R, w = au + bv } |
Notice that the span operator can be used in equations.
Example: Find a pair of vectors in R2 (not necessarily distinct) that solve the following equation:
The only solution is v = [0; 0], w = [0; 0].
We can also define setwise versions of the above properties. We reproduce them below, but we do not yet need to understand them. We will come back to them when we study vector spaces.
| property | definition |
| {w1, ..., wn, ...} are linear combinations of V {w1, ..., wn, ...} is the span of V span V = {w1, ..., wn, ...} |
{ w | ∃ a1,...,an ∈ R, v1,...,vn ∈ V, w = a1 v1 + ... + an vn } |
| {w1, ..., wn} are (setwise) linearly dependent | ∀ w ∈ {w1, ..., wn}, w ∈ span({w1, ..., wn} - w) |
| {w1, ..., wn} are (setwise) linearly independent | ∀ w ∈ {w1, ..., wn}, w ∉ span({w1, ..., wn} - w) |
| {w1, ..., wn} are (setwise) orthogonal | {w1, ..., wn} are pairwise orthogonal |
One thing we might choose to note: given what we know so far, how could we approach determining whether a given set of vectors is linearly independent? Is this approach practical or efficient?
Review of Notation: Logical formulas with quantifiers, sets, and set comprehensions.
Consult Section A.1 for a review of logical formulas and quantifiers, and Section A.2 for a review of set comprehensions.
Review: Problems with Vector Algebra
We review the operations and properties of vectors introduced in this section by considering several example problems.
Example: Given the points u = [x1,y1] and v = [x2,y2], find the equation of the line between these two points in the form y = mx + b.
We recall the definition for a line defined by two points:
Thus, if [x; y] is on the line, we have:
This implies the following system of equations (one from the x components in the above, and one from the y components):
| = |
| |||
| = |
|
If we solve for a in terms of x, we can recover a single equation for the line:
| = |
| |||
| = |
| |||
| = |
|
Notice that we can set m = (y1 - y2)/(x1 - x2) because that is exactly the slope of the line between [x1,y1] and [x2,y2].
| = |
| |||
| = |
|
We see that we can set b = - (m x1 + y1).
Example: Define the line that is orthogonal to the vector [x; y] but also crosses [x; y] (i.e, [x; y] falls on the line).
We know that the line must be parallel to the vector that is orthogonal to [x; y]. The line crossing [0; 0] that is orthogonal to [x; y] is defined as:
However, we need the line to also cross the point [x; y]. This is easily accomplished by adding the vector [x; y] to all the points on the orthogonal line going through [0; 0] (as defined above). Thus, we have:
Example: Is [7; -1] on the line defined by the points u = [19; 7] and v = [1; -5]?
To solve this problem, we recall the definition for a line defined by two points:
Thus, we want to know if [7; -1] is in the set defined as above. This can only occur if there exists an a such that [7; -1] = a (u - v) + u.
We solve for a; if no solution exists, then the point [7; -1] is not on the line L. If an a exists, then it is. In this case, a = 1/3 is a solution to both equations, so [7; -1] is on the line.
| = |
| |||
| = |
| ||||
| = |
| ||||
| = |
| |||
| = |
| |||
| = |
|
Example: Is [8; -6] a linear combination of the vectors [19; 7] and [1; -5]?
We recall the definition of a linear combination and instantiate it for this example:
Thus, if we can solve for a and b, then [8; -6] is indeed a linear combination.
| = |
| |||
| = |
| ||||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
|
Example: Given v = [15; 20], list the vectors that are orthogonal to v, but of the same length as v.
The two constraints on the vectors [x;y] we seek are:
| = |
| |||
| = |
|
We take the first constraint and solve for x in terms of y.
| = |
| |||
| = |
| |||
| = |
|
We now plug this into the second equation.
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
| |||
| = |
|
Thus, the vectors are (-20, 15) and (20,-15).
Example: Are the vectors [2; 1] and [3; 2] pairwise linearly independent?
There are at least two ways we can proceed in checking pairwise linear independence. Both involve checking if the vectors are linearly dependent. If they are linearly dependent, then they cannot be linearly independent. If they are not linearly dependent, they must be linearly independent.
We can compare the slopes; we see they are different, so they must be linearly independent.
We can also use the definition of linear dependence. If they are linearly dependent, then we know that
Does such an a exist? We try to solve for it:
| = |
| |||
| = |
| |||
| = |
| |||
| = |
|
Since we derive a contradiction, there is no such a, so the two vectors are not linearly dependent, which means they are linearly independent.
Example: Are the vectors V = {[2; 0; 4; 0], [6; 0; 4; 3], [1; 7; 4; 3]} pairwise linearly independent?
The definition for pairwise linear independence requires that all pairs of vectors being considered are linearly independent with each other. Thus, we must check all pairs. Because linear indepence of two vectors is a symmetric relation, we only need to consider 3!/2! = 3 combinations.
For each combination, we can check whether the pair is linearly dependent. If it is linearly dependent, we can stop and say that the three vectors are not linearly independent. If it is not, we must continue checking all the pairs. If all the pairs are not linearly independent, then the three vectors are pairwise linearly independent.
Notice that this an example of a general logical rule:
Note: This is the procedure for pairwise linear independence, which is distinct from setwise linear independence. In that case, we would need to apply the definition of setwise linear independence, which would mean that for each vector, we would need to determine whether it is a linear combination of the other two vectors.
We find that for all three pairs, assuming linear dependence leads to a contradiction.
| = |
| |||
| = |
| |||
| = |
|
| = |
| |||
| = |
| |||
| = |
|
| = |
| |||
| = |
| |||
| = |
|
Thus, V is pairwise linearly independent.
Example: Given constants a,b,c ∈ R, find a vector orthogonal to the plane defined by {(x,y,z) | a(x+y+z) + b(y+z) + cz = 0}.
We only need to rewrite the equation defining the plane in a more familiar form.
| = |
| |||
| = |
| |||
| = |
|
In order to be orthogonal to a plane, a vector must be orthogonal to all vectors (x,y,z) on that plane. Since all points on the plane are orthogonal to (a,b,c) by definition, (a,b,c) is such a point.
Applying Vectors and Linear Combinations to Problems
In the introduction we noted that in this course, we would define a symbolic language for working with a certain collection of idealized mathematical objects that can be used to model aspects of real-world problems in an abstract way. Because we are considering a particular collection of objects (vectors, planes, spaces, and their relationships), it is natural to ask what kinds of problems are well-suited for such a representation (and also what problems are not well-suited).
What situations and associated problems can be modelled using vectors and related operators and properties? Problems involving concrete objects that have a position, velocity, direction, geometric shape, and relationships between these (particularly in two or three dimensions) are natural candidates. For example, we have seen that it is possible to compute the projection of one vector onto another. However, these are just a particular example of a more general family of problems that can be studied using vectors and their associated operations and properties.
A vector of real numbers can be used to represent an object or collection of objects with some fixed number of characteristics (each corresponding to a dimension or component of the vector) where each characteristic has a range of possible values. This range could be a set of magnitudes (e.g., position, cost, mass), a discrete collection of states (e.g., absence or presence of an edge in a graph), or even a set of relationships (e.g., for every cow, there are four cow legs; for every $1 invested, there is a return of $0.02). Thus, vectors are well-suited for representing problems involving many instances of objects where all the objects have the same set of possible characteristics along the same set of linear dimensions. In these instances, many vector operations also have natural interpretations. For example, addition and scalar multiplication (i.e., linear combinations) typically correspond to the aggregation of a property across multiple instances or copies of objects with various properties (e.g., the total mass of a collection of objects).
In order to illustrate how vectors and linear combinations of vectors might be used in applications, we introduce the notion of a system. A system is any physical or abstract phenomenon, or observations of a phenomenon, that we characterize as a collection of real values along one or more dimensions. A state of a system is a particular collection of real values. For example, if a system is represented by R4, states of that system are represented by individual vectors in R4 (note that not all vectors need to correspond to valid or possible states; see the examples below).
Example: Consider the following system: a barn with cows and chickens inside it. There are several dimensions along which an observer might be able to measure this system (we assume that the observer has such poor eyesight that chickens and cows are indistinguishable from above):
- number of chickens inside
- number of cows inside
- number of legs that can be seen by peeking under the door
- number of heads that can be seen by looking inside from a high window
| = |
|
Given this relationship, it may be possible to derive some characteristics of the system given only partial information. Consider the following problem: how many chickens and cows are in a barn if 8 heads and 26 legs were observed?
| = |
|
Notice that a linear combination of vectors can be viewed as a translation from a vector describing one set of dimensions to a vector describing another set of dimensions. Many problems might exist in which the values are known along one set of dimensions and unknown along another set.
Example: We can restate the example from the introduction using linear combinations. Suppose we have $12,000 and two investment opportunities: A has an annual return of 10%, and B has an annual return of 20%. How much should we invest in each opportunity to get $1800 over one year?
The two investment opportunities are two-dimensional vectors representing the rate of return on a dollar:
|
The problem is to find what combination of the two opportunities would yield the desired observation of the entire system:
| = |
|
Next, we consider a problem with discrete dimensions.
Example: Suppose there is a network of streets and intersections and the city wants to set up cameras at some of the intersections. Cameras can only see as far as the next intersection. Suppose there are five streets (#1, #2, #3, #4, #5) and four intersections (A, B, C, and D) at which cameras can be placed, and the city wants to make sure a camera can see every street while not using any cameras redundantly (i.e., two cameras should not film the same street).
Vectors in R5 can represent which streets are covered by a camera. A fixed collection of vectors, one for each intersection, can represent what streets a camera can see from each intersection. Thus, the system's dimensions are:
- is street #1 covered by a camera?
- is street #2 covered by a camera?
- is street #3 covered by a camera?
- is street #4 covered by a camera?
- is street #5 covered by a camera?
- is there a camera at intersection A? (represented by the variable a below)
- is there a camera at intersection B? (represented by the variable b below)
- is there a camera at intersection C? (represented by the variable c below)
- is there a camera at intersection D? (represented by the variable d below)
|
Placing the cameras in the way required is possible if there is integer solution to the following equation involving a linear combination of the above vectors:
| = |
|
Example: Suppose a chemist wants to model a chemical reaction. The dimensions of the system might be:
- how many molecules of C3H8 are present?
- how many molecules of O2 are present?
- how many molecules of CO2 are present?
- how many molecules of H2O are present?
- how many atoms of carbon are present?
- how many atoms of hydrogen are present?
- how many atoms of oxygen are present?
Individual vectors in R3 can be used to represent how many atoms of each element are in each type of molecule being considered:
|
Suppose we know that the number of atoms in a system may never change during a reaction, and that some quantity of C3H8 and O2 can react to yield only CO2 and H2O. How many molecules of each compound will be involved in the reaction? That is the solution to the following linear combination.
| = |
|
The notion of a linear combination of vectors is common and can be used to mathematically model a wide variety of problems. Thus, a more concise notation for linear combinations of vectors would be valuable.
Matrices
Matrices and multiplication of a vector by a matrix
Matrices are a concise way to represent and reason about linear combinations and linear independence of vectors (e.g., setwise linear independence might be difficult to check using an exhaustive approach), reinterpretations of systems using different dimensions, and so on. One way to interpret a matrix is as a collection of vectors. Multiplying a matrix by a vector corresponds to computing a linear combination of that collection of vectors.
As an example, we consider the case for linear combinations of two vectors. The two scalars in the linear combination can be interpreted as a 2-component vector. We can then put the two vectors together into a single object in our notation, which we call a matrix.
| = |
|
Notice that the columns of the matrix are the vectors used in our linear combination. Notice also that we can now reinterpret the result of multiplying a vector by a matrix as taking the dot product of each of the matrix rows with the vector.
| = |
| ||||||||||||||||||||||||||
| = |
|
Because a matrix is just two column vectors, we can naturally extend this definition of multiplication to cases in which we have multiplication of a matrix by a matrix: we simply multiply each column of the second matrix by the first matrix and write down each of the resulting columns in the result matrix.
| = |
|
These definitions can be extended naturally to vectors and matrices with more than two components. If we denote using Mij the entry in a matrix M found in the ith row and jth column, then we can define the result of matrix multiplication of two matrices A and B as a matrix M such that
Interpreting matrices as tables of relationships and transformations of system states
We saw how vectors can be used to represent system states. We can extend this interpretation to matrices and use matrices to represent relationships between the dimensions of system states. This allows us to interpret matrices as transformations between system states (or partial observations of system states).
If we again consider the example system involving a barn of cows and chickens, we can reinterpret the matrix as a table of relationships between dimensions. Each entry in the table has a unit indicating the relationship it represents.
| chickens | cows | ||
| heads | 1 head/chicken | 1 head/cow | |
| legs | 2 legs/chicken | 4 legs/cow |
Notice that the column labels in this table represent the dimensions of an "input" vector that could be multiplied by this matrix, and the row labels specify the dimensions of the "output" vector that is obtained as a result. That is, if we multiply using the above matrix a vector that specifies the number of chickens and the number of cows in a system state, we will get a vector that specifies the number of heads and legs we can observe in that system.
| = |
|
Thus, we can interpret multiplication by this matrix as a function that takes system states that only specify the number of chickens and cows, and converts them to system states that only specify the number of heads and legs:
Interpreting multiplication of matrices as composition of system state transformations
Example: Suppose that we have a system with the following dimensions.
- number of wind farms
- number of coal power plants
- units of power
- units of cost (e.g., pollution)
- number of single family homes (s.f.h.'s)
- number of businesses
Two different matrices might specify the relationships between some combinations of dimensions in this system.
|
Notice that these two matrices both represent transformations between partial system state descriptions.
Notice that because the interpretion of a result obtained using the first transformation matches the interpretation of an input to the second, we can compose these transformations to obtain a third transformation.
This corresponds to multiplying the two matrices to obtain a third matrix. Notice that the units of the resulting matrix can be computed using a process that should be familiar to you from earlier coursework.
| = |
|
Thus, given some vector describing the number of wind farms and coal plants in the system, we can multiply that vector by (M2 ⋅ M1) to compute the number of single family homes and business we expect to find in that system.
Assignment #2: Matrix Algebra
In this assignment you will perform step-by-step algebraic manipulations involving vector and matrix properties and operations. For the word problems, you must solve them by setting up a system with dimensions, introducing a matrix characterizing the relationships between the dimensions in that system, and then solving for the system states that contain the information being sought in the problem statements.
-
- Finish the argument below that shows that matrix multiplication of vectors in R3 preserves lines.
∀ M ∈ R3×3, ∀ u,v,w ∈ R3, ∀ s ∈ R,
w = s(u-v) + v and
(w) is on the line defined by (u) and (v)
implies
# ...
(M w) is on the line defined by (M u) and (M v)
- Finish the argument below that shows that if multiplication by a matrix M maps three vectors to [0; 0; 0], it
maps any linear combination v' of those vectors to [0; 0; 0].
∀ M ∈ R3×3, ∀ u,v,w,v' ∈ R3, ∀ a,b,c ∈ R,
M u = 0 0 0 and M v = 0 0 0 and M w = 0 0 0 and v' = a u + b v + c w
implies
# ...
M v' = 0 0 0
Extra credit: if u, v, and w are setwise linearly independent, what can you say about the matrix M? Be as specific as possible.
- Show that if a matrix M in R2×2 is invertible, there is a unique solution for u given any equation M u = v with v ∈ R2.
∀ M ∈ R2×2, ∀ u,v ∈ R2,
(M) is invertible and
M u = v
implies
# ...
# replace the right-hand side below
# with an expression in terms of M and v
u = \undefined
- Show that if the column vectors of a matrix in R2×2 are linearly dependent, then its determinant is 0.
∀ a,b,c,d ∈ R,
( a c ) and ( b d ) are linearly dependent
implies
# ...
det a b c d = 0
Extra credit: you may include the opposite direction of this proof for extra credit (build a new, separate argument in which
det [a,c; c,d] = 0is found above theimpliesand`([a;c]) and ([b;d]) are linearly dependent`is at the end of the argument below it).
- Finish the argument below that shows that matrix multiplication of vectors in R3 preserves lines.
- In this problem, you will define explicit matrices that correspond to elementary row operations on matrices in R2×2.
- Find appropriate matrices A, B, C, and D in R2×2 to finish the following argument.
∀ A,B,C,D ∈ R2×2, ∀ a,b,c,d,t ∈ R,
A = \undefined and B = \undefined and C = \undefined and D = \undefined
implies
# ...
A a b c d = a+c b+d c d and B a b c d = a b c+a d+b and C a b c d = t⋅a t⋅b c d and D a b c d = a b t⋅c t⋅d
- Use the matrices A, B, C, and D from part (a) with matrix multiplication to construct a matrix E that can be
shown to satisfy the last line in the following argument.
∀ A,B,C,D,E ∈ R2×2, ∀ a,b,c,d,t ∈ R,
t = \undefined and A = \undefined and B = \undefined and C = \undefined and D = \undefined and E = \undefined
implies
# ...
E a b c d = c d a b
- Extra credit: the row operations defined by A, B, C, and D are all invertible as long as t ≠ 0;
prove this for t = -1 by showing that the matrices A, B, C, and D are invertible.
∀ A,B,C,D ∈ R2×2, ∀ t ∈ R,
t = -1 and A = \undefined and B = \undefined and C = \undefined and D = \undefined
implies
# ...
(A) is invertible and (B) is invertible and (C) is invertible and (D) is invertible
- Find appropriate matrices A, B, C, and D in R2×2 to finish the following argument.
-
You decide to drive the 2800 miles from New York to Los Angeles in a hybrid vehicle. A hybrid vehicle has two modes: using only the electric motor and battery, it can travel 1 mile on 3 units of battery power; using only the internal combustion engine, it can travel 1 mile on 0.1 liters of gas (about 37 mpg) while also charging the battery with 1 unit of battery power. At the end of your trip, you have 1400 fewer units of battery power than you did when you began the trip. How much gasoline did you use (in liters)?
You should define a system with the following dimensions:
- net change in the total units of battery power;
- total liters of gasoline used;
- total number of miles travelled;
- number of miles travelled using the electric motor and battery;
- number of miles travelled using the engine.
You should define a matrix in R3×2 to characterize this system. Then, write down an equation containing that matrix (and three variables in R), and solve it to obtain the quantity of gasoline.
∀ x,y,z ∈ R,
\undefined \undefined \undefined \undefined \undefined \undefined x y = \undefined \undefined \undefined
implies
# ...
z = \undefined
-
Suppose we create a very simple system for modelling how predators and prey interact in a closed environment. Our system has only two dimensions: the number of prey animals, and the number of predators. We want to model how the state of the system changes from one generation to the next.
If there are x predators and y prey animals in a given generation, in the next generation the following will be the case:
- all predators already in the system will stay in the system;
- all prey animals already in the system will stay in the system;
- for every prey animal, two new prey animals are introduced into the system;
- for every predator, two prey animals are removed from the system;
- we ignore any other factors that might affect the state (e.g., natural death or starvation).
-
Specify explicitly a matrix T in R2×2 that takes a description of the system state in one generation and produces the state of the system during the next generation. Note: you may simply enter the matrix on its own line for this part of the problem, but you must also use it in the remaining three parts below.
-
Show that the number of predators does not change from one generation to the next.
∀ T ∈ R2×2, ∀ x,y,y' ∈ R,
# replace \undefined with explicit matrix from part (a)
T = \undefined
implies
# ...
# In the conclusion below, you may replace y'
# with the correct expressionyou may NOT replace
# x.
T x y = x y'
Determine what initial state [x; y] is such that there is no change in the state from one generation to another.
∀ T ∈ R2×2, ∀ x,y ∈ R,
# replace \undefined with explicit matrix from part (a)
T = \undefined and x y = \undefined # find the explicit vector
implies
# ...
T x y = x y
Suppose that in the fourth generation of an instance of this system (that is, after the transformation has been applied three times), we have 2 predators and 56 prey animals. How many predators and prey animals were in the system in the first generation (before any transformations were applied)? Let [x; y] represent the state of the system in the first generation. Set up a matrix equation that involves [x; y] and matrix multiplication, and solve it to obtain the answer.
Matrix operations and their interpretations
The following table summarizes the matrix operations that we are considering in this course.
operation definition restrictions general properties M1 + M2 component-wise matrices must have
the same number of rows
and columnscommutative,
associative,
has identity (matrix with all 0 components),
has inverse (multiply matrix by -1),
scalar multiplication is distributiveM1 ⋅ M2 row-column-wise
dot productscolumns in M1 = rows in M2
rows in M1 ⋅ M2 = rows in M1
columns in M1 ⋅ M2 = columns in M2associative,
has identity I (1s in diagonal and 0s elsewhere),
distributive over matrix addition,
not commutative in general,
no inverse in general
M -1 columns in M = rows in M
matrix is invertibleM -1 ⋅ M = M ⋅ M -1 = I The following tables list some high-level intuitions about how matrix operations can be understood.
level of
abstractioninterpretations of multiplication
of a vector by a matrixapplications transformation of
system statesextraction of information
about system statescomputing properties of
combinations or aggregations
of objects (or system states)conversion of system
state observations
from one set of dimensions
to anothergeometry "moving" vectors in
a space (stretching,
skewing, rotating,
reflecting)projecting vectors taking a linear combination
of two vectorsreinterpreting vector notation
as referring to a collection
of non-canonical vectorslevel of
abstractioninterpretations of multiplication of two matrices applications composition of system state
transformations or conversionsgeometry sequencing of motions of vectors within
a space (stretching, skewing, rotating,
reflecting)level of
abstractioninvertible matrix singular matrix applications reversible transformation
of system statesextraction of complete
information uniquely determining
a system stateirreversible transformation
of system statesextraction of incomplete
information about
a system stategeometry reversible transformation or motion
of vectors in a spaceprojection onto a strict subset of
a set of vectors (space)symbolic reversible transformation of
information numerically encoded in matrix
(example of such information: system of
linear equations encoded as matrix)irreversible/"lossy" transformation of
information encoded in matrixSuppose we interpret multiplication of a vector by a matrix M as a function from vectors to vectors:
f(v) = M v.Fact: Notice that for any M, if f(v) = M v then f is always a function because M v has only one possible result (i.e., matrix multiplication is deterministic) for a given M and v.
Fact: If f(v) = M v, then f is invertible if M is an invertible matrix. The inverse of f is then defined to be:
f -1(v) = M -1 v.Notice that f -1 is a function because M -1 v only has one possible result. Notice that f -1 is the inverse of f because
f -1(f(v)) = M -1 M v = I v = v.Fact: If the columns of a matrix M are linearly dependent and f(v) = M v, then M cannot have an inverse. We consider the case in which M ∈ R2×2. Suppose we have that
M = a b c d . If the columns of M are linearly dependent, then we know that there is some s ∈ R such that
s a c = b d . This means that we can rewrite M:
M = a sa c sc . Since matrix multiplication can be interpreted as taking a linear combination of the column vectors, this means that for x,y ∈ R,
a sa c sc x y = a c x + sa sc y = (x + s y) a c But this means that for any two vectors (x,y) and (x',y'), if x + sy = x' + sy' then multiplying by M will lead to the same result. Thus, f is a function that takes two different vector arguments and maps them to the same result. If we interpret f as a relation and take its inverse f -1, f -1 cannot be a function. Thus, M cannot have an inverse (if it did, then f -1 would be a function).
Matrix properties
The following are subsets of Rn×n that are of interest in this course because they correspond to transformations and systems that have desirable or useful properties. For some of these sets of matrices, matrix multiplication and inversion have properties that they do not in general.
subset of Rn×n definition closed under
matrix
multiplicationproperties of
matrix multiplicationinversion identity matrix ∀ i,j
Mij = 1 if i=j, 0 otherwiseclosed commutative,
associative,
distributive with addition,
has identityhas inverse (itself);
closed under inversionelementary matrix can be obtained via an
elementary row operation
from I:- add multiple of one row
of the matrix to another
row - multiply a row by a
scalar - swap two rows of the
matrix
of the first two operations.associative,
distributive with addition,
have identityhave inverses;
closed under inversionscalar matrices ∃ s ∈ R, ∀ i,j
Mij = s if i=j, 0 otherwiseclosed commutative,
associative,
distributive with addition,
have identitynonzero members
have inverses;
closed under inversiondiagonal matrices ∀ i,j
Mij ∈ R if i=j, 0 otherwiseclosed associative,
distributive with addition,
have identitynonzero members
have inverses;
closed under inversionmatrices with
constant diagonal∀ i,j
Mii = Mjjassociative,
distributive with addition,
have identitysymmetric matrices ∀ i,j
Mij = Mjiassociative,
distributive with addition,
have identitysymmetric matrices
with constant diagonal∀ i,j
Mii = Mjj and Mij = Mjiclosed commutative,
associative,
distributive with addition,
have identityupper triangular matrices ∀ i,j
Mij = 0 if i > jclosed associative,
distributive with addition,
have identitynot invertible in general;
closed under inversion
when invertiblelower triangular matrices ∀ i,j
Mij = 0 if i < jclosed associative,
distributive with addition,
have identitynot invertible in general;
closed under inversion
when invertibleinvertible matrices M -1 M = M M -1 = I closed associative,
distributive with addition,
have identitynonzero members
have inverses;
closed under inversionsquare matrices all of Rn×n closed associative,
distributive with addition,
have identityTwo facts presented in the above table are worth noting.
Fact: Suppose A is invertible. Then the inverse of A -1 is A, because A A -1 = I. Thus, (A -1) -1 = A.
Fact: If A and B are invertible, so is AB. That is, invertible matrices are closed under matrix multiplication. We can show this by using the associativity of matrix multiplication. Since A and B are invertible, there exist B -1 and A -1 such that:
(B -1 A -1) A B = (B -1 A -1) A B = B -1 (A -1 A) B = B -1 I B = B -1 B = I. Thus, since there exists a matrix (B -1 A -1) such that (B -1 A -1) A B = I, (B -1 A -1) is the inverse of AB.
Another fact not in the table is also worth noting.
Fact: Any product of a finite number of elementary row matrices is invertible. This fact follows from the fact that all elementary matrices are invertible, and that the set of invertible matrices is closed under multiplication.
Given the last fact, we might ask whether the opposite is true: are all invertible matrices the product of a finite number of elementary matrices? The answer is yes, as we will see further below.
Solving the equation M v = w for M with various properties
Recall that for v,w ∈ Rn and M ∈ Rn×n, an equation of the following form can represent a system of equations:
M v = wNotice that if M is invertible, we can solve for v by multiplying both sides by M -1. More generally, if M is a member of some of the sets in the above table, we can find straightforward algorithms for solving such an equation for v.
M is ... algorithm to solve M v = w for v the identity matrix w is the solution an elementary matrix perform a row operation on M to obtain I;
perform the same operation on wa scalar matrix divide the components of w by the scalar a diagonal matrix divide each component of w by the
corresponding matrix componentan upper triangular matrix start with the last entry in v, which is easily obtained;
move backwards through v, filling in the values by
substituting the already known variablesa lower triangular matrix start with the first entry in v, which is easily obtained;
move forward through v, filling in the values by
substituting the already known variablesproduct of a lower triangular matrix
and an upper triangular matrixcombine the algorithms for upper and lower triangular
matrices in sequence (see example below)an invertible matrix compute the inverse and multiply w by it Example: We consider an equation M v = w where M is a diagonal matrix (the identity matrix and all scalar matrices are also diagonal matrices).
4 0 0 0 3 0 0 0 5 x y z = 2 9 10 4x = 2 3y = 9 5z = 10 x = 1/2 y = 3 z = 2 Example: We consider an equation M v = w where M is a lower triangular matrix.
4 0 0 2 4 0 4 3 5 x y z = 2 9 18 4x = 2 2x + 4y = 9 4x + 3y + 5z = 10 x = 1/2 y = 2 z = 2 Example: Suppose that M = L U where L is lower triangular and U is upper triangular. How can we solve M v = w?
First, note that because matrix multiplication is associative, we have
M v = (L U) v = L (U v) We introduce a new vector for the intermediate result U v, which we call u. Now, we have a system of matrix equations.
U v = u L u = w We first solve for u using the algorithm for lower triangular matrices, then we solve for v using the algorithm for upper triangular matrices.
Example: The inverse of a matrix in R2×2 can be computed as follows.
a b c d -1 = d/(ad-bc) -b/(ad-bc) -c/(ad-bc) a/(ad-bc) Thus, if we find that the determinant of a matrix M ∈ R2×2 is nonzero, the algorithm for solving M v = w is straightforward. Consider the following example.
1 2 3 4 x y = 5 13 1 2 3 4 -1 1 2 3 4 x y = 1 2 3 4 -1 5 13 1 0 0 1 x y = 4/((1⋅4)-(2⋅3)) -2/((1⋅4)-(2⋅3)) -3/((1⋅4)-(2⋅3)) 1/((1⋅4)-(2⋅3)) 5 13 1 0 0 1 x y = -2 1 3/2 1/-2 5 13 x y = 3 1 Row echelon form and reduced row echelon form
We define two more properties that a matrix may possess.
M is in row echelon form - all nonzero rows are above any rows consisting of all zeroes
- the first nonzero entry (from the left) of a nonzero row is strictly
to the right of the first nonzero entry of the row above it - all entries in a column below the first nonzero entry in a row are zero
(the first two conditions imply this)
M is in reduced row echelon form - M is in row echelon form
- the first nonzero entry in every row is 1; this 1 entry is the only nonzero entry in its column
We can obtain the reduced row echelon form of a matrix using a sequence of appropriately chosen elementary row operations.
Example: Suppose we want to find the reduced row echelon form of the matrix below. We list the steps of the procedure.
1 2 1 -2 -3 1 3 5 0 → 1 2 1 0 1 3 3 5 0 → 1 2 1 0 1 3 0 -1 -3 → 1 2 1 0 1 3 0 0 0 → 1 0 -5 0 1 3 0 0 0 Fact: For any matrix M, there may be more than one way to reach the reduced row echelon form using elementary row operations. However, it is always possible, and there is exactly one unique reduced row echelon form for that matrix M. We do not prove this result in this course, but fairly short proofs by induction can be found elsewhere (such as here). Because the reduced row echelon form of a matrix M is unique, we use the following notation to denote it:
rref M.Question: For a given matrix in reduced row echelon form, how many different matrices can be reduced to it (one or more than one)?
Fact: It is always true that rref M = rref (rref M). Thus, the rref operation is idempotent.
Fact: If rref M is I (the identity matrix), then M is invertible. This is because I is an elementary matrix, and the row operations used to obtain rref M from M can be represented as a product of elementary (and thus, invertible) matrices E1 ⋅ ... ⋅ En, so:
M = E1 ⋅ ... ⋅ En ⋅ I.Fact: If M ∈ Rn×n is not invertible, then the bottom row of rref M must have all zeroes. This is because when all rows of rref M ∈ Rn×n have nonzero values, it must be the identity matrix, and M must then be invertible.
Fact: The reduced row echelon form of an invertible matrix M ∈ Rn×n is I ∈ Rn×n.
We can show this is true using a proof by contradiction. Suppose that M is invertible, but rref M ≠ I. We know that rref M can be obtained via a finite number of elementary row operations E1 ⋅ ... ⋅ En:
(E1 ⋅ ... ⋅ En) M = rref M.If rref M is not I, then the last row of rref M must consist of only zeroes. But because M is invertible, we have:
((E1 ⋅ ... ⋅ En) M) M -1 = (rref M) M -1 E1 ⋅ ... ⋅ En = (rref M) M -1 Since the product of elementary matrices is invertible, (rref M) M -1 is also invertible. But if the last row of rref M consists of only zeroes, it cannot be that (rref M) M -1 is invertible. Thus, we have a contradiction, so our assumption that rref M ≠ I is false.
The above result implies the following fact.
Fact: If a matrix M is invertible, it is the finite product of a finite number of elementary matrices. This is because rref M is the identity, which is an elementary matrix, and M can be reduced via a finite number of invertible row operations to I. Thus, the elementary matrices can be used to generate every possible invertible matrix.
The following table summarizes the results.
fact justification (1) {M | M is a finite product of elementary matrices} = {M | rref M = I} I is an elementary matrix;
sequences of row operations
are equivalent to multiplication by
elementary matrices(2) {M | M is a finite product of elementary matrices} ⊂ {M | M is invertible} elementary matrices are invertible;
products of invertible matrices are invertible(3) {M | rref M = I} ⊂ {M | M is invertible} fact (1) in this table;
fact (2) in this table;
transitivity of equality(4) {M | M is invertible} ⊂ {M | rref M = I} proof by contradiction;
non-invertible M implies
rref M has all zeroes in bottom row(5) {M | M is invertible} = {M | rref M = I} for any sets A,B,
A ⊂ B and B ⊂ A
implies A = B(6) {M | M is a finite product of elementary matrices} = {M | M is invertible} fact (1) in this table;
fact (5) in this table;
transitivity of equalityGiven all these results, we can say that the properties for a matrix M in the following table are all equivalent: if any of these is true, then all of them are true. If any of these is false, then all of them are false.
M is invertible det M ≠ 0 the columns of M are (setwise) linearly independent Mv = w has exactly one solution M is a finite product of elementary matrices Fact: For matrices M ∈ Rn×n, rref M is guaranteed to be upper triangular. Notice that this means that for some finite product of elementary matrices E1 ⋅ ... ⋅ En, it is the case that
M = (E1 ⋅ ... ⋅ En) ⋅ U.If E1 ,..., En are all lower triangular, then then M has an LU decomposition. However, this will not always be the case.
Matrix transpose
Definition: The transpose of a matrix M ∈ Rn×n, denoted M⊤, is defined to be A such that Aij = Mji.
Fact: If a matrix M is scalar, diagonal, or symmetric, M⊤ = M. If a matrix M is upper triangular, M⊤ is lower triangular (and vice versa).
Fact: For A,B ∈ Rn×n, it is always the case that:
(A⊤)⊤ = A (A + B)⊤ = A⊤ + B⊤ s(B⊤) = (sB)⊤ Fact: It is always the case that (AB)⊤ = B⊤ A⊤. If M = AB, then:
(AB)ij = ith row of A ⋅ jth column of B = ith column of A⊤ ⋅ jth row of B⊤ = jth row of B⊤ ⋅ ith column of A⊤ = (B⊤ A⊤)ji. Fact: If A is invertible, then so is A⊤. This can be proven using the fact directly above.
∀ A,B ∈ R2×2,
(A) is invertible
implies
(A^(-1)) ⋅ A = 1 0 0 1 and A⊤ ⋅ (A^(-1))⊤ = ((A^(-1)) ⋅ A)⊤ and = 1 0 0 1 ⊤ and = 1 0 0 1
Fact: det A = det A⊤. We can see this easily in the A ∈ R2×2 case.
∀ a,b,c,d ∈ R,
det a b c d = a d-b c and = a d - c b and = det a c b d and det a b c d = det a c b d
Orthogonal matrices
Definition: A matrix M ∈ Rn×n is orthogonal iff M⊤ = M -1.
Fact: The columns of orthogonal matrices are always setwise orthogonal unit vectors. We can see this in the R2×2 case.
a b c d a b c d ⊤ = 1 0 0 1 a b c d a c b d = 1 0 0 1 (a,b) ⋅ (a,b) (a,b) ⋅ (c,d) (c,d) ⋅ (a,b) (c,d) ⋅ (c,d) = 1 0 0 1 . Below, we provide a verifiable argument for the R2×2 case.
∀ a,b,c,d ∈ R,
a b c d ⋅ a b c d ⊤ = 1 0 0 1
implies
a b c d ⋅ a c b d = 1 0 0 1 and a a + b b a c + b d c a + d b c c + d d = 1 0 0 1 and
a a + b b= 1 and a b ⋅ a b = 1 and || a b || = 1 and
( a b ) is a unit vector and
c c + d d = 1 and c d ⋅ c d = 1 and || c d || = 1 and
( c d ) is a unit vector and
a c + b d = 0 and a b ⋅ c d = 0 and
( a b ) and ( c d ) are orthogonal
Fact: Matrices representing rotations and reflections are orthogonal. We can show this for the general rotation matrix:
cos θ sin θ -sin θ cos θ cos θ sin θ -sin θ cos θ ⊤ = cos θ sin θ -sin θ cos θ cos θ -sin θ sin θ cos θ = cos 2 θ + sin 2 θ -cos θ sin θ + sin θ cos θ -sin θ cos θ + cos θ sin θ sin 2 θ + cos 2 θ = 1 0 0 1 . Fact: Orthogonal matrices are closed under multiplication. For orthogonal A, B ∈ Rn×n we have:
(AB)⊤ = B⊤ A⊤ = B -1 A -1 = (AB) -1. Fact: Orthogonal matrices are closed under inversion and transposition. For orthogonal A ∈ Rn×n we have:
(A -1)⊤ = (A⊤) -1. Thus, we can show that both A -1 and A⊤ are orthogonal.
(A -1)⊤ = (A -1) -1 (A⊤)⊤ = A. (A⊤)⊤ = (A⊤) -1 = A. We can summarize this by adding another row to our table of matrix subsets.
subset of Rn×n definition closed under
matrix
multiplicationproperties of
matrix multiplicationinversion orthogonal matrices M⊤ = M -1 closed associative,
distributive with addition,
have identitynonzero members
have inverses;
closed under inversionMatrix rank
Yet another way to characterize matrices is by considering their rank.
Definition: We can define a the rank of a matrix M, rank M, as the number of nonzero rows in rref M.
We will see in this course that rank M is related in many ways to the various characteristics of a matrix.
Fact: Matrix rank is preserved by elementary row operations. Why is this the case? Because rref is idempotent and rank is defined in terms of it:
rref M = rref (rref M) number of nonzero rows in rref M = number of nonzero rows in rref (rref M) rank (M) = rank (rref M) Fact: If M ∈ Rn×n is invertible, rank M = n. How can we prove this? Because all invertible matrices have rref M = I, and I has no rows with all zeroes. If I ∈ Rn×n, then I has n nonzero rows.
Fact: For A ∈ Rn×n, rank A = rank (A⊤). We will not prove this in this course in general, but typical proofs involve first proving that for all A ∈ Rn×n, rank A ≤ rank (A⊤). Why is this sufficient to complete the proof? Because we can apply this fact for both A and A⊤ and use the fact that (A⊤)⊤ = A:
rank(A) ≤ rank(A⊤) rank(A⊤) ≤ rank((A⊤)⊤) rank(A⊤) ≤ rank(A) rank(A⊤) = rank(A) To get some intuition about the previous fact, we might consider the following question: if the columns of a matrix M ∈ R2×2 are linearly independent, are the rows also linearly independent?
Fact: The only matrix in Rn×n that has no nonzero rows in reduced row echelon form is I.
Fact: If a matrix M ∈ Rn×n has rank n, then it must be that rref M = I (and, thus, M is invertible). This is derived from the fact above.
Fact: Invertible matrices are closed under the transposition operation. In other words, if M is invertible, then M⊤ is invertible. How can we prove this using the rank operator? We know that rank is preserved under transposition, so we have:
n = rank(A) = rank(A⊤) = n Thus, the rank of rank(A⊤) is n, so it is invertible.
The following table summarizes the important facts about the rank and rref operators.
rank (rref M) = rank M rref (rref M ) = rref M rank (M⊤) = rank M for M ∈ Rn×n, M is invertible iff rank M = n Matrix similarity
We introduce a relation on matrices called similarity in order to practice some matrix algebra. We will use the notion of similarity later in the course in other ways.
Definition: We can define a relation on matrices called similarity. Two matrices A and B in Rn×n are similar, which we write as
A ∼ B,iff there exists an invertible matrix C such that
A = C -1 B C.The relation ∼ is reflexive, symmetric, and transitive.
Fact: For any A ∈ Rn×n,
A = I A I -1 A ∼ A so the relation ∼ is reflexive.
Fact: For any A,B ∈ Rn×n, if A ∼ B then we have C ∈ Rn×n such that
A = C -1 B C C (A) C -1 = C (C -1 B C) C -1 C (A) C -1 = (C C -1) B (C C -1) C (A) C -1 = B B = C A C -1 B = (C -1) -1 A (C -1). Thus, there exists an invertible matrix, namely C -1, that satisfies the definition for similarity, so B ∼ A.
Fact: For any X,Y,Z ∈ Rn×n, if X ∼ Y and Y ∼ Z then we have X ∼ Z:
X = C -1 Y C Y = D -1 Z D X = C -1 (D -1 Z D) C X = (C -1 D -1) Z (D C) We know that invertibility is closed under multiplication and (D C) -1 = C -1 D -1, so D C is the invertible matrix that satisfies the definition for similarity between X and Z:
X = (D C) -1 Z (D C) Notice that because all invertible matrices can be expressed as a finite product of elementary matrices. So if two matrices are similar, does it mean they have the same reduced row echelon form? No. We can provide a counterexample.
Review #1
This section contains a comprehensive collection of review problems going over the course material covered until this point. These problems are an accurate representation of the kinds of problems you may see on an exam.
Problem: Find any h ∈ R such that the following two vectors are linearly independent.
5 -5 -2 , 20 -20 h There are many ways to solve this problem. One way is to use the definition of linear dependence and find an h that does not satisfy it.s 5 -5 -2 = 20 -20 h Then, we have that any h such that h ≠ -8 is sufficient to contradict linear dependence (and, thus, imply linear independence):
s ⋅ 5 = 20 s = 4 s ⋅ (-2) = h -8 = h Another solution is to recall that orthogonality implies linear independence. Thus, it is sufficient to find h such that the two vectors are orthogonal.
5 -5 -2 ⋅ 20 -20 h = 0 This implies h = 100.
5(20) + (-5)(-20) + (-2)h = 0 h = 100 Problem: Suppose we have a matrix M such that the following three equations are true:
M 1 0 0 = 3 -2 M 0 1 0 = 3 0 M 0 0 1 = -3 1 Compute the following:
M 2 1 -1 = ? We should recall that multiplying a matrix by a canonical unit vector with 1 in the ith row in the vector gives us the ith column of the matrix. Thus, we can immediately infer that:M = 3 3 -3 -2 0 1 Thus, we have:
M ⋅ 2 1 -1 = (3,3,-3) ⋅ (2,1,-1) (-2,0,1) ⋅ (2,1,-1) = 12 -5 Problem: List at least three properties of the following matrix:
0 1 0 1 0 0 0 0 1 The matrix has many properties, such as:- it is an elementary matrix
- it is an invertible matrix
- it is an orthogonal matrix
- it is a symmetric matrix
- it has rank n
- its reduced row echelon form is the identity
Problem: List all unit vectors orthogonal to:
4 -3 It is sufficient to solve for (x,y) that satisfy the following equations:x y ⋅ 4 -3 = 0 ||(x,y)|| = 1 Problem: List all the unit vectors that are linearly dependent with:
5 12 It is sufficient to solve for s and (x,y) that satisfy the following equations:s x y = 5 12 ||(x,y)|| = 1 One approach is to write x and y in terms of s and then solve for s using the second equation.
Problem: Find the matrix B ∈ R2×2 that is symmetric, has a constant diagonal, and satisfies
B 2 1 = 15 6 We know that B is symmetric and has a constant diagonal, so we need to solve for a and b in:a b b a ⋅ 2 1 = 15 6 Problem: Compute the inverse of the following matrix:
2 3 1 2 One approach is to set up the following equation and solve for a,b,c, and d:a b c d ⋅ 2 3 1 2 = 1 0 0 1 Another approach is to apply the formula for the inverse of a matrix in R2×2:
2 3 1 2 -1 = (1 / (2 ⋅ 2 - 3 ⋅ 1)) ⋅ 2 -3 -1 2 = 2 -3 -1 2 Problem: Let a ∈ R be such that a ≠ 0. Compute the inverse of the following matrix:
a -a -a -a As in the previous problem, we can either solve an equation or apply the formula:a -a -a -a -1 = (1 / (-a2 - a2)) ⋅ -a a a a Problem: In terms of a, b ∈ R where a ≠ 0 and b ≠ 0, compute the inverse of:
a 0 0 b a 0 0 b a 0 0 b a 0 0 b While we could perform the instances of matrix multiplication step-by-step and then invert the result (either by solving an equation or using the formula for the inverse of a matrix in R2×2), it's easier to recall that diagonal matrices behave in a manner that is very similar to the real numbers. Thus, the above product is equal toa4 0 0 b4 , and its inverse simply has the multiplicative inverses of the two diagonal entries as its diagonal entries:
1/a4 0 0 1/b4 . Problem: Let A ∈ R2×2 be an orthogonal matrix. Compute A A⊤ A.
We recall that because A is orthogonal, A⊤ = A -1. Thus, we have thatA A⊤ A = (A A -1) A = I A = A.The following problems are slightly more difficult. Only one or two such problems would be found on an exam.
Problem: Suppose x ∈ R is such that x ≠ 0. Compute the inverse of the following matrix:
x 0 -2x 0 x 0 0 0 4x Because we have an upper triangular matrix, computing the inverse by solving the following equation is fairly efficient. Start by considering the bottom row and its product with each of the columns. This will generate the values for g, h, and i. You can then proceed to the other rows.x 0 -2x 0 x 0 0 0 4x a b c d e f g h i = 1 0 0 0 1 0 0 0 1 The solution is:
1/x 0 1/(2x) 0 1/x 0 0 0 1/4x Problem: Given an invertible upper triangular matrix M ∈ R2×2, show that M -1 is also upper triangular. Hint: write out the matrix M explicitly.
Suppose we have the following upper triangular matrix:M = x y 0 z If it is invertible, then there exists an inverse such that:
x y 0 z ⋅ a b c d = 1 0 0 1 This implies that
xa + yb = 1 xc + yd = 0 zc = 0 zd = 1 Because M is invertible, we know that z ≠ 0. Since zc = 0, This means that c = 0. Thus, we have that the inverse is upper triangular.
Problem: Find a matrix that is not the identity matrix, but is similar only to itself. Explain why it cannot be similar to any other matrix.
The only such matrix is:M = 0 0 0 0 It cannot be similar to any other matrix because for any invertible matrix C, C -1 M C will be M. Thus, the set of all matrices similar to M is {M}:
{A | A ∈ R2×2, A ~ M} = {M}Problem: Find a matrix that is similar but not equivalent to the following matrix:
M = 2 4 1 2 It suffices to pick a non-trivial invertible matrix E, such as an elementary matrix, and compute E -1 M E. One option is:E -1 M E = 1 1 0 1 2 4 1 2 1 -1 0 1 = 3 3 1 2 Problem: Suppose that a gram of gold costs $50, while a gram of silver costs $10. After purchasing some of each, you have spent $350 on 15 grams of material. How many grams of each commodity have you purchased?
- Write down four dimensions describing this system.
- grams of gold
- grams of silver
- cost
- total weight in grams
-
Define a matrix A that can be used to convert a description of a system state that specifies only the amount of gold and silver purchased into
a description of the system state that specifies only the cost and total weight.
A = 1 1 50 10 - Write down a matrix equation describing this problem and solve it to find the solution.
1 1 50 10 ⋅ x y = 15 350 x y = 5 10 -
Define a matrix B such that for any description of a system state v that specifies only the total weight and amount spent, Bv
is a description of that system state that specifies the amount of gold and silver in that system state.
We are looking for the inverse of A.
A -1 = -1/4 1/40 5/4 -1/40 -
Suppose that the per gram price of gold and silver were the same. What can you say about the properties of the matrix A?
The matrix M is not invertible (it is singular).
Vector Spaces
Sets of vectors and their notation
We are interested in studying sets of vectors because they can be used to model sets of system states (and, thus, entire systems), observations and data that might be obtained about systems, geometric shapes and regions, and so on. As we did with vectors and matrices, we can introduce a symbolic language for sets of vectors consisting of symbols, operators, and predicates. And, as with vectors and matrices, we can study the algebraic laws that govern symbolic expressions.
We will consider three kinds of sets of vectors in this course; they are listed in the table below.
kind of set (of vectors) maximum
cardinality
("quantity of
elements")solution space of a... examples finite set of vectors finite - {(0,0)}
- {(2,3),(4,5),(0,1)}
vector space infinite homogenous system of
linear equations:
Av = 0- {(0,0)}
- R
- R2
- span{(1,2),(2,3),(0,1)}
- any point, line, or plane
intersecting the origin
affine space infinite nonhomogenous
system of
linear equations:
Av = w- { a + v | v ∈ V} where
V is a vector space and a is a vector - any point, line, or plane
To represent finite sets of vectors symbolically, we adopt the convention of simply listing the vectors between a pair of braces (as with any set of objects). However, we need a different convention for symbolically representing vector spaces and affine spaces. This is because we must use a symbol of finite size to represent a vector space or affine space that may contain an infinite number of vectors.
We first recall the definition for what constitutes a vector space (there are many equivalent definitions).
Definition: A vector space is a set of vectors that contains 0, is closed under vector addition and scalar multiplication, and is such that all the elements in the set satisfy the vector space axioms governing vector addition and scalar multiplication.
Fact: Any set of linear combinations of a collection of vectors is closed under vector addition and scalar multiplication, contains 0, and satisfies the vector space axioms. In other words, for any collection of vectors v1, ..., vn, span{v1, ..., vn} is a vector space.
Fact: For any set of vectors V in Rn×n that satisfies the vector space axioms, there exists a finite set of at most n vectors v1, ..., vk (where k ≤ n) such that span{v1, ..., vk} = V.
Given the two facts above, we can safely adopt span{v1, ..., vn} as a standard notation for vector spaces. In addition to this notation, we will also often use the notation Rn for specific values of n (e.g., R2 is equivalent to span{[1;0],[0;1]}), and {0} for specific vector 0 (e.g., {[0;0]} is equivalent to span{[0;0]}).
Equality of sets of vectors and vector spaces
Recall that many of the algebraic laws we saw governing operators on vectors and matrices involved equality of vectors and matrices. In fact, one can view these laws as collectively defining the semantic equality of the symbols (i.e., they specify when two symbols refer to the same object). Thus, the meaning of these symbols is closely tied to the equality relation we define over them.
Because we are considering sets of vectors, and equality of pairs of vectors has already been defined, it is relatively straightforward to provide a definition of equality for sets of vectors (both finite and infinite).
Definition: We have the following definitions:
w ∈ V iff ∃ v ∈ V, v = w W ⊂ V iff ∀ w ∈ W, w ∈ V W = V iff W ⊂ V and V ⊂ W It is easy to use the above to compute whether two finite sets of vectors are equivalent. However, while the above definition is mathematically adequate for any two infinite sets of vectors (including vector spaces), it does not help us define a practical algorithm for computing equality for our chosen notation for vector spaces (spans of finite sets of vectors). Suppose we take the definition above and replace the vector spaces with explicit spans of finite sets of vectors.
Definition: Let W and V be finite sets of vectors.
w ∈ span V iff ∃ v ∈ span V, v = w (1) span W ⊂ span V iff ∀ w ∈ span W, w ∈ span V (2) span W = span V iff span W ⊂ span V and span V ⊂ span W (3) We still have a problem: how do we try all possible vectors w in span W (see the ∀ quantifier on the right-hand side of the statement (2))? This can be addressed by observing that if w1,...,wn ∈ V, then span w1,...,wn ∈ V. Thus, it is sufficient to check that the finite number of vectors in W are found in V.
There is another problem. How do we determine whether a given vector w is in the vector space that we call span V? Notice that determining this is equivalent to determining whether w is a linear combination of the vectors in V (we assume that the size of the finite set V is n). Because V is finite set of n vectors, we can always find a matrix MV that has the vectors in V as its columns.
w ∈ span V iff w ∈ {v | ∃ a1,...,an ∈ R, v1,...,vn ∈ V, v = a1v1 + ... + anvn } iff ∃ a1,...,an ∈ R, v1,...,vn ∈ V, w = a1v1 + ... + anvn iff ∃ x ∈ Rn, MV ⋅ x = w Thus, determining whether w ∈ span V is equivalent to determining whether there is a solution to the equation MV ⋅ x = w. We can solve such equations in general by building an augmented matrix and then finding its reduced row echelon form.
Example: Consider the following example of how one can solve an equation Mv = w by finding the reduced row echelon form of an augmented matrix.
M := 1 2 4 5 6 8 -3 1 4 w := 4 5 8
rref \augment(M,w) # the solution x to Mx=wWe have now found a process that allows us to determine for a particular W and V whether span W = span V:
span W = span V iff span W ⊂ span V and span V ⊂ span W span W ⊂ span V iff ∀ w ∈ span W, w ∈ span V ∀ w ∈ span W, w ∈ span V iff ∀ w ∈ W, w ∈ span V w ∈ span V iff ∃ x ∈ Rn, MV ⋅ x = w The above implies that a matrix can be used to represent a particular vector space. We will see in other sections further below that a given vector space can be represented in more than one way by a matrix, and that more than one matrix can be used to represent a vector space.
Vector spaces as abstract structures
Our definitions of a vector space so far have explicitly referenced sets of concrete vectors as we usually understand them. However, this is not necessary.
Definition: A vector space is a set of objects S such that
- there is a unique additive identity 0 ∈ S
- addition (+) is an operation on elements of S under which S is closed, and which satisfies the vector space axioms
- scalar multiplication (⋅) is an operation on elements of S under which S is closed, and which satisfies the vector space axioms
The above definition specifies conditions under which any set of objects S can be studied as a vector space.
Fact: The affine space A = {a + v | v ∈ V} is a vector space for appropriate definitions of addition, scalar multiplication, and identity.
- addition (⊕) can be defined as follows. It is an operation on elements of A under which A is closed, and which satisfies the vector space axioms:
v ⊕ w = u where u = (v - a) + (w - a) + a = v + w - 2a + a = v + w - a.
- scalar multiplication (⊗) can be defined as follows. It is an operation on elements of A under which A is closed,
and which satisfies the vector space axioms:
s ⊗ v = u where u = (s ⋅ (v - a)) + a = sv - sa + a = sv + (1-s)a.
- there is a unique additive identity in A; it is the vector a:
v ⊕ a = v + a - a = v.
An abstract definition of vector spaces is useful because it also allows us to study by analogy and learn about other objects that are not necessarily sets of vectors. All the properties we can derive about vector spaces using the above definition will apply to other sets of objects that also satisfy the above definition.
Example: We consider the set of functions F = {f | f(x) = cx, c ∈ R}. How do we show that F is a vector space?
- there is a unique additive identity in F: f(x) = 0x
- addition (+) is an operation on elements of F under which F is closed, and which satisfies the vector space axioms:
f + g = h where h(x) = f(x) + g(x)
- scalar multiplication (⋅) is an operation on elements of F under which F is closed, and which satisfies the vector space axioms:
s ⋅ f = h where h(x) = s ⋅ f(x)
Exercise: Show that {f | f(x) = bx2 + cx, b,c ∈ R} is a vector space.
Exercise: Find two elements in {f | f(x) = bx2 + cx + d, b,c,d ∈ R} that are linearly independent. What does it mean for two functions to be linearly independent?
Exercise: What is a finite set of functions that spans {f | f(x) = bx2 + cx + d, b,c,d ∈ R}? One such set is:
{f,g,h} where f(x) = 1, g(x) = x, h(x) = x2Example: We consider the set of functions {f | f(x) = xk, k ∈ R}. The following definitions of addition and scalar multiplication make this set of functions a vector space.
- there is a unique additive identity: f(x) = x0
- addition (+) is defined as:
f + g = h where h(x) = f(x) ⋅ g(x)
- scalar multiplication (⋅) is an operation on elements of S under which S is closed, and which satisfies the vector space axioms:
s ⋅ f = h where h(x) = f(x)s
Example: Just as with any vector space, we can set up and solve problems involving linear combinations of vectors. Suppose we want to find a function in the space {f | f(x) = ax3 + bx2 + cx + d, a,b,c,d ∈ R} that fits a certain collection of points, such as:
{(1,3), (-1,13), (2,1), (-2,33)}We can interpret each point as a pair (x, f(x)). We can then set up the following system of equations:
f(1) = 3 f(-1) = 13 f(2) = 1 f(-2) = 33 Expanding, we have:
a(1)3 + b(1)2 + c(1) + d = 3 a(-1)3 + b(-1)2 + c(-1) + d = 13 a(2)3 + b(2)2 + c(2) + d = 1 a(-2)3 + b(-2)2 + c(-1) + d = 33 Notice that we can rewrite this in the form of an equation M v = w:
(1)3 (1)2 (1) 1 (-1)3 (-1)2 (-1) 1 (2)3 (2)2 (2) 1 (-2)3 (-2)2 (-2) 1 ⋅ a b c d = 3 13 1 33 This shows us that we can interpret individual objects in {f | f(x) = ax3 + bx2 + cx + d, a,b,c,d ∈ R} as vectors in R4. We can also view this problem in terms of systems, system states, and observations. If the function f(x) = ax3 + bx2 + cx + d that solves the above system is a state of the system, then (3, 13, 1, 33) is a partial observation of that state along four distinct "dimensions".
Note that finding the equation for a line that crosses two points is just a special case of the above.
Example: We want to find a function f(x) = cx + d such that the points (2,3) and (5,-4) fall on the line the equation represents. Thus, we have:
(2) 1 (5) 1 ⋅ c d = 3 -4 We can consider many spaces of functions beyond spaces of polynomial functions. For example, suppose exp(x) = ex. Then we can define the following vector space:
span{ exp, cos , sin }.We can also generalize this approach to families of related functions.
Example: Consider the following set of vectors of functions, where f' denotes the derivative of a function f:
F = { (f, f, f') | f(x) = bx2 + cx + d }The set F is a vector space. Now, suppose we have the following problem. Find the function for a parabola in F such that (1,4) and (2,-3) lie on the parabola, and the maximum or minimum point on the parabola is at x = 1. Such a function is represented by the solution to the following equation:
(1)2 (1) 1 (2)2 (2) 1 2(1) 1 0 ⋅ b c d = 4 -3 0 Note that the number of rows in the matrix (and result vector) corresponds to the number of data points for which a model is being sought, and is not bounded.
Example: Find the order 5 polynomial that exactly fits the points [-1;45], [8;4], [6;5], [2;-8], [-10;8], [15;6].
P := {
-1 45 ,
8 4 ,
6 5 ,
2 -8 ,
-10 8 ,
15 6 } M := (\augment { x^5, x4, x3, x2, x, 1 ⊤ | x y ∈ P })⊤ C := (\augment { y | x y ∈ P })⊤ B := \augment (M, C) A := rref B The disadvantage to using this particular approach to fitting functions to data points is that the data must match an actual function perfectly (or, equivalently, the space of functions being considered must be rich enough to contain a function that can fit the data points exactly). We will see further below how to find functions that have the "best" fit (for one particular definition of "best") without necessarily matching the points exactly.
Subspace relation on vector spaces
Definition: Given two vector spaces W and V, we have:
W is a (vector) subspace of V iff V ⊂ W.Finding a basis and an orthonormal basis of a vector space
We have adopted span{v1,...,vn} as our notation for vector spaces. However, this makes it possible to represent a given vector space in a variety of ways:
span{(0,1),(1,0)} = span{(0,1),(1,0),(1,0)} = span{(0,1),(1,0),(1,0),(1,0)}, and so on.We might naturally ask: given a vector space V, what is the smallest possible size for a finite set of vectors W such that V = span W?
Definition: A finite set of vectors B is a basis of the vector space V if span B = V and for all finite sets of vectors W such that span W = V, |B| ≤ |W|.
Fact: A finite set of vectors v1,...,vn is a basis for V iff span {v1,...,vn} = V and the vectors v1,...,vn are setwise linearly independent.
Fact: Given a finite set of vectors v1,...,vn, we can find the basis for span {v1,...,vn} by creating a matrix M in which the rows are the vectors v1,...,vn and computing rref M. The set of distinct nonzero rows in rref M is a basis for span {v1,...,vn}.
Example: Below, we find the basis of span {[-3;0;7;0], [-9;0;21;0], [0;0;2;8], [0;0;1;4], [3;0;13;4], [0;0;1;0]}.
A := \augment{ -3 0 7 0 , -9 0 21 0 , 0 0 2 8 , 0 0 1 4 , 3 0 13 4 , 0 0 1 0 } B := A⊤ \decompose ((rref B)⊤) - { 0 0 0 0 } Definition: A finite set of vectors B is an orthonormal basis of the vector space V if B is a basis of V, all the vectors in B are unit vectors, and the vectors in B are setwise orthogonal.
Recall that for any vector v ∈ Rn and any unit vector u ∈ Rn, (v ⋅ u) ⋅ u is the projection of v onto the line parallel to u (i.e., the vector space {a u | a ∈ R}). We can use this fact to define a process for turning an arbitrary basis into an orthonormal basis.
Fact: Given a basis B = {v1,...,vn}, it is possible to turn it into an orthonormal basis by using the Gram-Schmidt process. This algorithm can be summarized as follows.
u1 = v1 e1 = u1 / ||u1 || u2 = v2 - ((v2 ⋅ e1) ⋅ e1) e2 = u2 / || u2 || u3 = v3 - ((v3 ⋅ e1) ⋅ e1) - ((v3 ⋅ e2) ⋅ e2) e3 = u3 / || u3 || u4 = v4 - ((v4 ⋅ e1) ⋅ e1) - ((v4 ⋅ e2) ⋅ e2) - ((v4 ⋅ e3) ⋅ e3) e4 = u4 / || u4 || ⋮ un = vn - Σi = 1n-1 ((vn ⋅ ei) ⋅ ei) en = un / || un || Intuitively, for each vector vi ∈ B, the algorithm substracts out the contributions of the already-computed orthogonal unit vectors from vi, obtaining ui, and then rescales ui to make it into a unit vector.
Many computational environments for mathematics that support linear algebra provide an operator for turning a basis into an orthonormal basis. An example is provided below.
\orthonormal { 4 0 , 1 2 } Why is an orthonormal basis useful? Once again, we appeal to the fact that (v ⋅ u) ⋅ u is the projection of v onto u, where v ⋅ u is the length of that projection. Suppose we want to determine how to express an arbitrary vector v using an orthonormal basis u1,...,un.
Fact: Given a vector v ∈ Rn, and an orthonormal basis B = {u1,...,un} for Rn, we can determine what linear combination of the vectors u1,...,un yields v by computing:
a = (MB)⊤ ⋅ v.Notice that the components of the vector a, which we will call a1,...,an, are the scalars needed to compute v as a linear combination of the vectors u1,...,un:
v = a1 u1 + ... + an un = MB a.Fact: Given a vector v ∈ Rn, some k < n, and an orthonormal basis B = {u1,...,uk} for a subspace W ⊂ Rn, the product (MB ⋅ (MB)⊤ ⋅ v) is the projection of v onto W.
Example: Notice the relationship of the above fact to projection onto the span of a single unit vector u = (x,y) in R2. Suppose we have a basis B = {u} for a subspace {s ⋅ u | s ∈ R2} ⊂ R2. Then we have
Thus, for an arbitrary v ∈ R2 not necessarily in {s ⋅ (x,y) | s ∈ R2} we have:MB = x y MB ⋅ (MB)⊤ ⋅ v = x y ⋅ x y ⊤ ⋅ v = x y ⋅ ( x y ⋅ v ) = ( x y ⋅ v ) ⋅ x y = ( v ⋅ x y ) ⋅ x y = ( v ⋅ u ) ⋅ u Thus, we see that the projection of a vector onto another unit vector in R2 is just a special case of the general approach to projection.
Assignment #3: Vector SpacesIn this assignment you will work with vector spaces, including vector spaces of functions.
-
- Use the appropriate operators to calculate a basis for the following vector spaces.
V1 := span {
3 2 5 0 8 ,
1 0 -6 7 5 ,
0 0 1 0 1 ,
-6 -4 -10 0 -16
}V2 := span {
1 0 -4 0 ,
2 0 3 1 ,
1 0 -6 7 ,
0 0 1 0 ,
4 0 8 -5 ,
-1 0 -1 0
}V3 := span { 1 3 -9 , -2 -6 18 , 4 0 0 } S1 := { 3 2 5 0 8 , 1 0 -6 7 5 , 0 0 1 0 1 , -6 -4 -10 0 -16 } S2 := { 1 0 -4 0 , 2 0 3 1 , 1 0 -6 7 , 0 0 1 0 , 4 0 8 -5 , -1 0 -1 0 } S3 := { 1 3 -9 , -2 -6 18 , 4 0 0 } \decompose ((rref (\augment S1)⊤)⊤) - { 0 0 0 0 0 } \decompose ((rref (\augment S2)⊤)⊤) - { 0 0 0 0 } \decompose ((rref (\augment S3)⊤)⊤) - { 0 0 0 } - Complete the following argument showing that span{ [1;2], [2;4] } = span {[3;6]} using the propositions provided in the verifier. Hint:
find an explicit vector x ∈ R2 and add it to the second premise in place of undefined; use a similar approach (and a similar
but distinct proposition) when building the part of the argument for the other direction of ⊂.
∀ x ∈ R2,
x = \undefined # Find an explicit vector to put here.
implies
# ...
\augment ( 1 2 , 2 4 ) ⋅ x = 3 6 and # Hint (keep this in your argument).
# ...
span{ 1 2 , 2 4 } = span { 3 6 }
∀ x ∈ R2,
{ 1 2 , 2 4 } ⊂ span { 3 6 } and
\augment ( 1 2 , 2 4 ) ⋅ x = 3 6 and x = 1 1
implies
\augment ( 1 2 , 2 4 ) ⋅ 1 1 = 3 6 and 3 6 ∈ span { 1 2 , 2 4 } and { 3 6 } ⊂ span { 1 2 , 2 4 } and span{ 1 2 , 2 4 } ⊂ span { 3 6 } and span { 3 6 } ⊂ span{ 1 2 , 2 4 } and span{ 1 2 , 2 4 } = span { 3 6 } - Complete the following argument: show that the assumptions imply that the spans are equivalent.
∀ a,b,c,d,v,v',w,w' ∈ R2, ∀ A,B ∈ R2×2,
A = \augment(w,w') and B = \augment(v,v') and A ⋅ a = v and A ⋅ b = v' and B ⋅ c = w and B ⋅ d = w'
implies
# ...
span {w,w'} = span {v,v'}
∀ a,b,c,d,v,v',w,w' ∈ R2, ∀ A,B ∈ R2×2,
A = \augment(w,w') and B = \augment(v,v') and A ⋅ a = v and A ⋅ b = v' and B ⋅ c = w and B ⋅ d = w'
implies
\augment(w,w') ⋅ a = v and \augment(w,w') ⋅ b = v' and \augment(v,v') ⋅ c = w and \augment(v,v') ⋅ d = w' and v ∈ span {w,w'} and v' ∈ span {w,w'} and w ∈ span {v,v'} and w' ∈ span {v,v'} and {v,v'} ⊂ span {w,w'} and {w,w'} ⊂ span {v,v'} and span {v,v'} ⊂ span {w,w'} and span {w,w'} ⊂ span {v,v'} and span {w,w'} = span {v,v'}
- Use the appropriate operators to calculate a basis for the following vector spaces.
-
Find the order 9 polynomial that exactly fits the following data. Your solution must be in the form of a vector in R10 that represents the coefficients of the polynomial.
P := {
-1 31 ,
-4 268327 ,
1 17 ,
-5 -1520701 ,
3 389147 ,
-3 78869 ,
-6 -19979509 ,
5 29571949 ,
0 -1 ,
-2 5027 } Hint: you can make your answer shorter by using a comprehension to generate a one-row matrix containing the different powers of x. For example:
x := 2
\augment (
xk | k ∈ {0 ... 9})
P := {
-1 31 ,
-4 268327 ,
1 17 ,
-5 -1520701 ,
3 389147 ,
-3 78869 ,
-6 -19979509 ,
5 29571949 ,
0 -1 ,
-2 5027 }
# This is the right-hand side of the equation.w := (\augment ( y | x y ∈ P))⊤
# We generate the matrix using a nested comprehension.S := ( (\augment ( x^(9-k) | k ∈ {0 ... 9}))⊤ | x y ∈ P )
# This is the matrix in the left-hand side of the equation.
M := (\augment S)⊤
# The matrix is invertible, so we can multiply both sides
# of the equation by the inverse of M to obtain the
# solution.
(M^(-1)) ⋅ w
# Alternatively, we can find the rref of the augmented
# matrix.
rref \augment(M,w)
# The solution vector has the x9 coefficient as its first entry.
# If we had usedxk instead of x^(9-k) in our formula for S,
# this would be reversed.
- Consider the order 3 polynomial f(x) = 2x3 + 5x2 - 3x + 1.
-
Find the order 2 polynomial that is the closest least squares approximation of f on the set {-2,0,2,4,8,16}.
{ 2 (x3) + 5 (x2) - 3 x + 1 | x ∈ {-2,0,2,4,8,16} } - Compute the error of the approximation from part (a) above on the domains {-2,0,2,4,8,16} and {-16,-8,-4,-2,-1,0}.
Solution to #3 (both parts):
# The points to which we're trying to find an approximately
# fitting function.Points3a := { x 2 (x3) + 5 (x2) - 3 x + 1 | x ∈ {-2,0,2,4,8,16} }
# The right-hand side of the overdetermined system.v := (\augment { y ⊤ | x y ∈ Points3a })⊤
# The matrix on the left-hand side of the overdetermined system.M := (\augment { x2, x, 1 ⊤ | x y ∈ Points3a})⊤
# The orthonormal matrix that can be used to compute projections
# onto the span of the columns of M.
A := \augment \orthonormal \decompose (rref M⊤)⊤
# The projection of v onto the span of the columns of M.
w := A ⋅ A⊤ ⋅ v
# Part (a):
# The solution to the system below contains the coefficients
# for the least squares approximation. The top entry corresponds
# to the x2 coefficient.
FullMatrix := rref \augment (M, w)
# We could isolate the actual coefficients in a 3-component
# vector, but this is not required.approx := (\augment (\decompose ((FullMatrix ⋅ 0 0 0 1 )⊤) - { 0 }))⊤
# Part (b):
# The error on the initial domain is defined as follows.
||v - w||
# Below is an alternative formula.
||v - M ⋅ approx||
# To compute the error of the approximation on the second
# domain, we must first generate the points and build the
# corresponding matrix:Points3b := { x 2 (x3) + 5 (x2) - 3 x + 1 | x ∈ {-16,-8,-4,-2,-1,0} } M3b := (\augment { x2 x 1 ⊤ | x y ∈ Points3b})⊤
# Then, M3b ⋅ approx gives us the outputs of the function
# on the new data points. We compute the error in the same way.
||v - M3b ⋅ approx||
Homogenous, non-homogenous, overdetermined, and underdetermined systems
While we have usually considered n × n matrices, in real-world applications (especially those involving data), system states usually have a shorter description than the corpus of data (e.g., observational data) being used to determine the system state. Thus, problems in such applications usually involve matrices in which the number of rows is very different from the number of columns. Furthermore, the data may be noisy, which means that there may be no exact system state that matches the data. Informally, this might mean that the system of equations being used to determine a system state is overdetermined. On the other hand, if the amount of data is not sufficient to determine a single system state, a system is underdetermined.
Definition: For any matrix M ∈ Rn×m and vector v ∈ Rm, the system M x = v is overdetermined if there exist no solutions to the equation M x = v.
Definition: For any matrix M ∈ Rn×m and vector v ∈ Rm, the system M x = v is undetermined if there exist two or more solutions for x that satisfy the equation M x = v.
Definition: For any matrix M ∈ Rn×m, the system M x = 0 is homogenous.
Definition: For any matrix M ∈ Rn×m and vector v ∈ Rm where v ≠ 0, the system M x = v is nonhomogenous.
Fact: A homogenous system M x = 0 has at least one solution.
Fact: A homogenous system M x = 0 is never overdetermined.
Fact: The solution space of a homogenous system is a vector space:
- there is a unique additive identity: 0 is a solution
- adding two solutions yields a solution:
M x = 0 M y = 0 M (x + y) = M x + M y = 0 - multiplying a solution by a scalar yields a solution:
M x = 0 M (s y) = s (M y) = s 0 = 0
Fact: The solution space of a nonhomogenous system is an affine space.
Motivating Example: Suppose we have a nonhomogenous system M x = v where v ∈ R1000000.
We may not know ahead of time whether or not it is overdetermined. Suppose we do not want to incur the cost of attempting to solve M x = v exactly. This might be because we only want to make one pass of the data to reduce costs, but it might also be because this is a data stream that is too voluminous to store, so the data will be gone unless we solve the system right away (e.g., data from a telescope, a particle collider, or Twitter).
In such cases, we can typically assume the data will have noise, so the system is overwhelmingly likely to be overdetermined and have no solution. Thus, we are okay with finding an approximate solution.
We do know, however, that M x = 0 has at least one solution, and that the solution space is a vector space (so, for example, we could try to "search" for a better solution using some other technique involving addition and scalar multiplication once we find at least one non-trivial one). Thus, we might instead choose to solve the system M x = 0, knowing that even in the worst case, a very poor approximate solution of 0 will always be found in the worst case.
Is there a better compromise between these two strategies of keeping v or changing it to 0? Can we find some other space of solutions that won't be overdetermined, but will still allow us to find a non-trivial (nonzero) approximate solution? One possibility is to project the vector v onto a subspace of the solution space, ensuring that the system is no longer overdetermined. This approach is covered in the section below.
Application: approximating overdetermined systems
Fact: We first review the triangle inequality in the case of a right triangle. Suppose we have a triangle with a height a, a base length of b, and a hypotenuse of length c. Then we have:
a2 + b2 ≥ a2 c2 ≥ a2 c ≥ a This implies that the orthogonal projection of a vector v ∈ V onto a subspace W ⊂ V is the closest point in W to v.
Definition: Given v ∈ V and a subspace W ⊂ V, the vector w within the subspace W that is closest to v is a vector w* ∈ W such that ||v - w*|| is minimal. In other words, for all w' ∈ W,
||v - w*|| ≤ ||v - w'||.Definition: Given v ∈ V and a subspace W ⊂ V, the orthogonal projection of v onto W is the closest vector in W to v.
We can show the above is true by appealing to the above fact related to the triangle inequality.
Fact: Let B = {w1,...,wn} be a basis for W ⊂ V. Recall that MB is the matrix whose columns are the vectors in B. Given v ∈ V where v ∉ W, MB x = v has no solution. This is because MB x ∈ span B; thus, if a solution existed, we would have v ∈ span B and v ∈ W, which contradicts our assumption.
Fact: Let B = {w1,...,wn} be an orthonormal basis for W ⊂ V. Given v ∈ V, the error of an approximate solution x to the equation MB x = v is defined to be
||v - MB x||.Fact: Let B = {w1,...,wn} be a basis for W ⊂ V. Given v ∈ V, the approximate solution x* to the equation MB x = v with smallest error is defined to be the least-squares approximate solution to MB x = v. In other words, the least-squares approximate solution x* to MB x = v is such that for any other x',
||v - MB x*|| ≤ ||v - MB x'||.Why is it called a "least-squares" approximation?
Fact: Let B = {w1,...,wn} be a basis for W ⊂ V. Given v ∈ V and its projection w* ∈ W, the least-squares approximate solution to MB x = v is the solution x* to the system
MB x* = w*.That is, if we assume the above equality, then for all possible and x' and w' = MB x', we have that:
||v - MB x*|| ≤ ||v - MB x'|| ||v - w*|| ≤ ||v - w'|| In the table below, we summarize the correspondences used in the above facts.
concept related to
solving MB x = vnotation relationship notation geometric concept the space of values W with
which we can replace v in
the overdetermined system MB x = v
to make a system MB x = w
that has solutions{MB x | x ∈ Rn} the span of the
columns of MBspan B the subspace W of V
spanned by Bthe error of an approximate
solution x' to MB x = v||v - MB x' || MB x' = w' ||v - w'|| the distance between
w' ∈ W and v ∈ VMB x* where x* is
the minimum error solution
to MB x = vfor all x',
||v - MB x* || ≤ ||v - MB x' ||MB x* = w* for all w' ∈ W,
||v - w*|| ≤ ||v - w'||the orthogonal projection
w* of v ∈ V onto W
(the closest vector in W
to v)Notice that we know a solution to MB x = w* exists, and that we can show this in two different ways. Since w* ∈ W, it must be that w is a linear combination of the vectors in B, so it is a linear combination of the columns in MB. Alternatively, if MB is a square matrix and we know that B is a basis, then the columns of MB are linearly independent, which means MB is invertible, so
x* = MB -1 w*.Fact: We can compute the least-squares solution to any equation M x = v by using the following process:
- find an orthonormal basis B of the span of the column vectors of M to make MB
- use MB to compute the projection w* of v onto span B
- solve the system M x = w* by finding the rref of an augmented matrix
Later in the course we will consider a slightly different way of solving this problem that uses algebraic properties of linear transformations.
Exercise: Suppose a matrix M is such that M x = 0 has exactly one solution. What can we say about the error of the least-squares approximation of any system M x = v?
Exercise: Suppose a matrix M is such that M x = 0 has Rn as its space of solutions. What can we say about any system M x = v? What can we say about the error of any least-squares approximation of a solution for M x = v?
Exercise: We know that the solution space for an undetermined system Mx = 0 is a vector space. Thus, this space must have a basis. How can we use a process similar to the Gram-Schmidt algorithm to find a basis of this space?
Relationship to curve fitting and linear regressions in statistics
The method described above does overlap with standard curve fitting and linear regression techniques you see in statistics. There are many variants to these approaches, and the one considered above corresponds to a fairly basic variant that has no specialized characteristics (i.e., it makes no special assumptions about the data points, the relative importance of the data points, their distribution, or the way they can be interpreted).
- The approach above is known as ordinary least squares and as linear least squares.
- The case in which the function space is {f | f(x) = ax + b, a,b ∈ R} corresponds to a simple linear regression. This involves fitting a line to a collection of points while minimizing the sum of the squares of the distances parallel to the y-axis between all the data points and the approximate line. This diagram is an illustration of this. The method in these notes is more general in that it is not restricted to polynomials of order 1, but can be used to fit polynomials of any order to data.
-
We can restate the least squares method described in these notes as finding x* such that
the vector ε in M x* = v - ε is minimized. Notice that ε + w = v.
The length of the vector ε can be viewed as the sum of squares of y-axis-aligned distances from the
estimate curve to the actual data points:
||ε|| = ||v - M x*||.
- This diagram illustrates the projection method being used.
- The matrix M in M x = v is sometimes called the design matrix. The same term is used to refer to the corresponding matrix in a simple linear regression.
Application: approximating a model of system state dimension relationships
The approach described in the previous section can be used to approximate a solution to the equation M x = v. Usually, if M describes a model of a system (in this sense, system refers to a system of states that are described by values along some number of dimensions, as in an earlier section), solving M x = v corresponds to determining a system state x given some other information about a system state v.
What if we instead have a large collection of pairs of observations of system states of the form (x,v) (or, more generally, any collection of observations of a system along multiple dimensions). Can we approximate a model of a set of relationships between some two subsets of the dimensions in the system? In other words, if we take all our observations (x1, ..., xn) and divide them into pairs of descriptions x = (x1,...,xk) and v = (xk+1,...,xn), can we find the best M that approximates the relationship between incomplete system state descriptions x and v?
Example: Suppose we have the following dimensions in our system:
- number of red dwarf stars
- number of G type stars
- number of pulsars
- units of infrared (IR) radiation observed
- units of ultraviolet (UV) radiation observed
- units of gamma (γ) radiation observed
Suppose that we already have some set of confirmed (but possibly noisy) observations of systems along all the dimensions (the dimensions of the quantities in each point correspond to the list of dimensions above):
O := {
4 5 1 243 3341 700 ,
3 6 21 125 1431 1465 ,
4 2 13 533 3432 334 ,
16 4 4 334 143 762 ,
13 8 13 235 1534 513 ,
34 16 17 333 3532 450
}For the above observations, we want to find a matrix that relates the first three dimensions (the number of each type of star) to the last three dimensions (the amount of each kind of radiation). In other words, we are looking for a matrix M ∈ R3× 3 of the form:
a units IR/red dwarf b units IR/G type c units IR/pulsar d units UV/red dwarf e units UV/G type f units UV/pulsar g units γ/red dwarf h units γ/G type i units γ/pulsar Multiplication by the above matrix represents a system state description transformation with the following units:
(# red dwarf stars, # G type stars, # pulsars) → (units IR, units UV, units γ)We can split the data into two collections of points: those that specify the number of each type of star (the inputs to the above transformation), and those that specify the amount of each kind of radiation (the output of the above transformation). Below, we call these P and Q. We then turn these two sets of data points into matrices. In order to turn this problem into the familiar form M x = v, we transpose the two matrices.
O := {
4 5 1 243 3341 700 ,
3 6 21 125 1431 1465 ,
4 2 13 533 3432 334 ,
16 4 4 334 143 762 ,
13 8 13 235 1534 513 ,
34 16 17 333 3532 450
}P := { a b c | a b c x y z ∈ O} Q := { x y z | a b c x y z ∈ O}
M := (\augment P)⊤
v := (\augment Q)⊤ # Actually a matrix.
A := \augment \orthonormal \decompose (rref M⊤)⊤
w := A ⋅ (A⊤) ⋅ v
rref \augment (M, w)The dimension of a vector space
Definition: The dimension of a vector space V, which we write as dim V, is the size of the basis for V.
Example: What is the dimension of {f | f(x) = ax3 + bx2 + cx + d, a,b,c,d ∈ R}?
Example: Consider the vector space consisting of finite sets of real numbers:
- there is a unique additive identity: {}
- addition (+) is defined as:
P + T = Q where Q = P ∪ T
- scalar multiplication is defined as:
s ⋅ T = Q where Q = {s ⋅ r | r ∈ T}
Orthogonal complements of vector spaces
Definition: The orthogonal complement W⊥ of a vector subspace W ⊂ V is the set of all vectors in V that are orthogonal to all the vectors in W:
W⊥ = {v | v ∈ V, ∀ w ∈ W, v ⋅ w = 0}Notice that the orthogonal complement of a subspace is always taken within the context of some specified space V.
Algebra of vector spaces
In this section, we consider vector spaces, their orthogonal complements, and common set operations: set union, set intersection, and set product.
Exercise: Given any two vectors spaces V and W, is V ∪ W a vector space? No. For example, consider
V = span{[1;0]} ∪ span{[0;1]}.We have that [1;0] ∈ V and [0;1] ∈ V, but not [1;0] + [0;1] = [1;1] ∈ V.
Exercise: Given any two vectors spaces V and W, is V ∩ W a vector space? Yes.
- there is a unique additive identity: 0 ∈ V and 0 ∈ W, so 0 ∈ V ∩ W
- V ∩ W is closed under addition (+): if v,w ∈ V ∩ W then we have that v ∈ V and w ∈ V, and we also have that
v ∈ W and w ∈ W, so we have that
v + w ∈ V and v + w ∈ W, so v + w ∈ V ∩ W.Since addition satisfies the vector space axioms for elements V and W, it also does so for elements in V ∩ W.
- V ∩ W is closed under scalar multiplication (⋅): if v ∈ V ∩ W then we have that v ∈ V and w ∈ V, so we have that
sv ∈ V and sv ∈ W, so sv ∈ V ∩ W.
Since scalar multiplication satisfies the vector space axioms for elements V and W, it also does so for elements in V ∩ W.
Exercise: Given any two vectors spaces V and W, is V × W a vector space? Yes.
- there is a unique additive identity: (0V,0W) where 0V ∈ V and 0W ∈ W
- there is an addition operation (+):
(v,w) + (v',w') = (v+v', w+w')
- there is a scalar multiplication (⋅) operation:
s (v,w) = (sv, sw)
Exercise: For a vector space W ⊂ V, compute W ∩ W⊥.
Fact: For a vector subspace W ⊂ V,
dim W + dim W⊥ = dim V.Fact: For a vector subspace W ⊂ V,
W × W⊥ = V.
Linear Transformations
Maps (a.k.a., functions) and their properties
In addition to the definitions involving relations and maps we introduce in the Appendix, we consider several more definitions.
First, we introduce a notation for specifying the set of inputs a function accepts, and the set of outputs it may produce. We use the notation
f: A → Bto indicate that a function takes elements in the set A and maps them to elements in the set B. This notation is equivalent to
f ∈ A → Bwhere A → B is the set of functions that map elements from A to elements in B:
A → B = { f | ∀ a ∈ A, f(a) ∈ B }.Definition: Given a map f: A → B, we call A the domain of f.
Definition: Given a map f: A → B, we call B the codomain of f. We can also call it the range of f, but this can be ambiguous (because sometimes it is used to refer to the image, defined below) so we avoid using it.
We also introduce some properties of a map that can be used to describe more precisely describe its set of outputs and the relationship between those outputs and the inputs the can generate them.
Definition: Given a map f: A → B, we call {f(a) | a ∈ A} the image of f.
Definition: Given a map f: A → B, for any subset A' ⊂ A, we call {f(a) | a ∈ A'} the image of A' under f. We sometimes write this as f(A).
Definition: Given a map f: A → B, for any a ∈ A, we call f(a) the image of a under f.
Definition: Given a map f: A → B, for any subset B' ⊂ B, we call {a | a ∈ A, f(a) ∈ B} the pre-image of B under f. We sometimes write this as f -1(B).
Definition: Given a map f: A → B, for any b ∈ B, we call {a | a ∈ A, f(a) = b} the pre-image of b under f. We sometimes write this as f -1(b).
Finally, we consider a few properties of maps that deal with how the map relates elements in its domain to elements in its codomain.
Definition: A map f: A → B is surjective (or onto) if for all b ∈ B, there exists a ∈ A such that f(a) = b.
Definition: A map f: A → B is injective (or one-to-one) if for all a,a' ∈ A, f(a) = f(a') implies a = a'.
Definition: A map f: A → B is bijective if it is surjective and injective.
Visual illustrations of examples of the above definitions can be found in the Appendix.
Fact: A map f: A → B is injective iff for all a,a' ∈ A, a ≠ a' implies f(a) ≠ f(a'). We can prove this by appealing to the logical fact that given two propositions P and Q, not P implies not Q iff Q implies P.
Fact: If B is the codomain of f, B' is the image of f, and f is surjective, then B = B'.
Fact: If f: A → B is bijective, then f -1 is bijective.
Fact: If f: A → B is not injective, then f -1 is not a function. If f is not injective, then there exist a,a' ∈ A such that a ≠ a' but f(a) = f(a'). In this case, we cannot define a single value to which f -1(f(a)) can evaluate, so f -1 cannot be a function.
Exercise: Describe with as much detail as you can the domains, codomains, and images of the following maps (there is more than one right answer for these, as the definitions do not specify the domains of the functions). Determine whether each map is injective, surjective, or both given the domains and codomains you chose.
f(x) = 3x f(x) = x2 f(x) = -x f(x) = x ⋅ √(-1) f(x) = x 0 0 x f( M, N ) = M ⋅ N where M and N are matrices f( x y ) = 1 2 3 4 x y Fact: Given some f:A → B, the following process can be used to show a map f is injective:
- assume a,a' ∈ A and a ≠ a';
- it is necessary to show that f(a) ≠ f(a'):
- expand f(a) and f(a') using the definition of f,
- use algebraic properties or other facts to derive f(a) ≠ f(a').
- assume a,a' ∈ A;
- assume f(a) = f(a'):
- expand f(a) and f(a') using the definition of f,
- use algebraic properties or other facts to derive a = a'.
Fact: Given some f:A → B, we can show a map f is not injective by picking some explicit a,a' ∈ A such that a ≠ a' and showing that f(a) = f(a'). Alternatively, pick some explicit b ∈ B and find two or more distinct solutions a and a' ∈ A to the equation f(x) = b.
Fact: Given some f:A → B, the following process can be used to determine whether a map f is surjective:
- let b ∈ B;
- solve f(x) = b:
- if you can solve the equation (or derive an equation x = g(b)) such that x ∈ A, f:A → B is surjective,
- if the equation has no solutions in A, f:A → B is not surjective.
Exercise: Show that f: R → R where f(x) = x + 1 is injective.
Exercise: Show that f: R → R where f(x) = x + 1 is surjective.
Definition: Given two maps f: B → C and g: A → B, we define the composition of f and g, which we denote f o g, as the map h:A → C defined by:
h(x) = f(g(x))Exercise: Show that if f: B → C and g: A → B are injective, then their composition (f o g):A → C is injective.
Homomorphisms and isomorphisms
The previous section defined a number of properties of functions f: A → B that only address the equality of elements in A and B. However, what if A and B have relations and operators? For example, what if A and B are vector spaces with an identity, an addition operation, and a scalar multiplication operation?
We can restrict our notion of a map or function to maps or functions f: A → B that somehow preserve or consistently transform the properties of operators and relations we may have already defined on A and B. For example, suppose we have A = {a1, a2, a3}, B = {b1, b2, b3}, an operator ⊕ such that a1 ⊕ a2 = a3, and an operator ⊕ over elements of B such that b3 ⊕ b2 = b1. A map f from A to B that preserves (or respects, or consistently transforms) ⊕ would be such that
f(a3) = b1 f(a2) = b2 f(a1) = b3 Notice that the above map is such that the operation ⊕ is respected by the map f:
f(a3) = f(a1 ⊕ a2) = f(a1) ⊕ f(a2) = b3 ⊕ b2 = b1 Definition: Given a binary operator ⊗ over A and another operator ⊕ over B, we say that a map f: A → B is a homomorphism if we have that
∀ a,a' ∈ A, f(a ⊗ a') = f(a) ⊕ f(a').Notice that a homomorphism might have, but does not necesserily have, any of the properties we introduced for maps: it could be injective, surjective, and so on.
Definition: A bijective homomorphism f: A → B is called an isomorphism.
Linear transformations
In this course we are interested in a specific kind of homomorphism.
Definition: For any two vector spaces V and W, a map f: V → W is a linear transformation iff we have that for all v,v' ∈ V and scalars s ∈ R,
f(v + v') = f(v) + f(v') f(s ⋅ v) = s ⋅ f(v) In other words, a linear transformation is a homomorphism between vector spaces that preserves vector addition and scalar multiplication. If a map f does not satisfy the above properties, it is not a linear transformation.
Fact: For any linear transformation f:A → B and appropriate constants 0 ∈ A and 0' ∈ B,
f(0) = 0'We can show this in the following way: given any v ∈ V,
0 = 0 ⋅ v f(0) = f(0 ⋅ v) = 0 ⋅ f(v) = 0' Fact: For any linear transformation f:A → B and the corresponding additive inversion operations of A and B, it is the case that f respects additive inversion:
f(-v) = -f(v)We can derive this fact in two ways. One approach is to use the previous fact that f(0) = 0' to show that f(-v) is indeed the inverse of f(v):
f(v) + f(-v) = f(v + (-v)) = f(0) = 0' The other approach is to use the fact that in both vector spaces, v = -1 ⋅ v:
v = 1 ⋅ v v + (-1 ⋅ v) = (1 ⋅ v) + ((-1) ⋅ v) = (1 + (-1)) ⋅ v = 0 ⋅ v = 0 Then, because f respects scalar multiplication, we have that:
f(-1 ⋅ v) = -1 ⋅ f(v) Thus, the argument is:
f(v) + f(-v) = f(v) + f(-1 ⋅ v) = f(v) + ((-1) ⋅ f(v)) = f(v) + (-f(v)) = 0 Fact: For any two linear transformations f: V → W, g: U → V, the composition f o g: U → W is also a linear transformation. To show this, we must demonstrate that if h(x) = f(g(x)) then h respects vector addition and scalar multiplication. For any u,u' ∈ U, and s ∈ R, we have:
h(v + v') = f(g(v + v')) = f(g(v) + g(v')) = f(g(v)) + f(g(v')) = h(v) + h(v') and
h(s ⋅ v) = f(g(s ⋅ v)) = f(s ⋅ g(v)) = s ⋅ f(g(v)) = s ⋅ h(v) Because linear transformations are homomorphisms (and, thus, maps), we can ask whether they have properties of maps (i.e., whether they are injective, surjective, bijective, and so on). We will do so further below.
Data modelling as a linear transformation
Recall that for a system that can be described using quantities along multiple dimensions, subsets of a vector space Rn can be used to model that system's possible states (or observations of that system's states). Recall also that a matrix can be used to model the relationships between the dimensions describing that system, and that finding an approximate model of such relationships involves finding a matrix in a vector space of matrices.
In a similar manner, linear transformations (and, more generally, homomorphisms) can be used to represent the relationship between actual data from (or observations of) a system, and possible mathematical models of that system. The problem of finding a mathematical model of data in a domain D can be viewed as the problem of finding an appropriate mathematical structure M and an appropriate homomorphism (or isomorphism) f:D → M from the data domain D to that mathematical model. If we assume that the data domain can be modelled using a vector space, then M can be a vector space and f can be a linear transformation.
Example: As an illustration, we consider a very simple (and fairly contrived) example from chemistry. Suppose we have three substances: iron (I), sulfur (S), and troilite (T). Through experiments, we find that mixing 8 units of iron and 1 unit of sulfur (together with some energy) produces 8 units of troilite. We write this down as:
8 I ⊕ 1 S = 8 T.We could take our data and define a set with a an operation ⊕ that corresponds to whatever we do to produce the chemical reaction:
S = {I, S, T, 2 I, 2 S, 2 T, 3 I, 3 S, 3 T, ...} 8 I ⊕ 1 S = 8 T 16 I ⊕ 2 S = 16 T ⋮ We do not know the internal structure of individual units of iron, sulfur, and troilite. Even if individual units of each can be represented using multiple dimensions, we do not know how many dimensions there might be and what those dimensions might represent.
Nevertheless, we can make hypotheses about what structure might be appropriate to model this system. We can then test these hypotheses by using them to make new predictions and collecting data to verify or negate those predictions.
We hypothesize that there exists a non-trivial vector space V with a vector addition operation + such that we can construct a homomorphism from our data to V. We assume it is non-trivial (nonzero) because a trivial space like this always exists: let I, S, and T all map to 0 ∈ V. We are looking for a vector space V and homomorphism f such that
f(8 I ⊕ 1 S) = f(8 I) + f(1 S) = 8 f(I) + 1 f(S) = 8 f(T)Thus, we are looking V with non-trivial (nonzero) u, v, w ∈ V such that:
8 u + 1 v = 8 wHow many dimensions should V have in order for our model to be interesting? What is the minimum number of dimensions V must have so that u, v, and w are nonzero? What number of dimensions would make it trivially easy to find u, v, and w that fit the above equation?
We choose dim V = 2 and V = R2. We can also make some additional assumptions to simplify our problem: let u and v be orthogonal and axis-aligned. Then we have the following equation:
8 x 0 + 1 0 y = 8 a b Thus, we have that:
x = a y = 8 b Assume that a = 1 and b = 1, we get x = 1 and y = 8. Thus, we have found u,v, and w ∈ R2 such that f respects ⊕ by mapping it to +:
f(I) = 1 0 f(S) = 0 8 f(T) = 1 1 Notice that we made several assumptions, but this is okay. We can test the quality and fitness of these assumptions later by making predictions and collecting more data. This corresponds to the usual scientific method: hypothesize what kind of mathematical model fits the data, add assumptions until the model is instantiated to match or approximate the data (the model should not be so simple that it can fit any data, or so complex that it only fits the already collected data), make a prediction using the model about something which has not yet been observed, and try to confirm or falsify that prediction by collecting more data.
How do we interpret the two dimensions of V? We do not necessarily know when we first create the model to fit the data. They may correspond to actual entities, or they may correspond to abstract characteristics that can be broken down further once more data is collected. In this case, they happen to correspond to the number of iron and sulfur atoms in the molecules of iron, sulfur, and troilite.
What is a prediction we can make using our model? Let us consider a scenario in which we introduce a different mix of iron and sulfur into our reaction; how much troilite do we expect to make? We can write down the equation:
8 I + 2 S = c TApplying our homomorphism, we get:8 1 0 + 2 0 8 = c 1 1 This implies:
8 + 0 = c 0 + 2 ⋅ 8 = c Since there is no solution, our model predicts that it is not possible to convert all 8 units of iron and all 2 units of sulfur into troilite. This negative prediction is already testable, but we can do better by looking for a more positive prediction. Our mathematical model V is a vector space, and this suggests that the right-hand side of the equation must represent a linear combination of the three vector f(I), f(S), and f(T). This suggests we could write down a slightly different equation:
8 1 0 + 2 0 8 = c 1 1 + d 1 0 + e 0 8 This implies:
8 + 0 = c + d 0 + 2 ⋅ 8 = c + 8 e Notice that there exist multiple solutions to these equations. Which correspond to reasonable interpretations within the physical system we are modelling? All three variables should be positive; we might also require that they should be integers, and that c is nonzero. We have that
e = (16-c)/8,so c is either 16 or 8. It cannot be 16 because d > 0, so c = 8. Thus, e = 1 and d = 0. This predicts that 8 units of iron and 2 units of sulfur should produce 8 units of troilite and 1 unit of sulfur. This is a testable prediction that we can use to direct further experiments to evaluate the quality of the model.
We will see similar examples in later sections.
Kernels of linear transformations
Definition: For a linear transformation f:A → B, the kernel of f of the set of elements in the domain of f that map to 0 ∈ B:
ker f = {a | a ∈ A, f(a) = 0 }.Fact: For a linear transformation f:A → B, is the case that:
- ker f ⊂ A
- the image of ker f under f is {0}
- ker f is the pre-image of 0 under f
Definition: For a linear transformation f:A → B, ker f is a vector space (and, thus, a subspace of A). How do we show this formally?
Exercise: Suppose we are given the linear transformation f:R4 → R3 defined as:
f( x y z t ) = x + y z + t 0 . What is the codomain of f? What is the image of f? What is the kernel of f? Provide a set comprehension to define each.
Exercise: Suppose we are given the linear transformation f:R4 → R4 defined as:
f( x y z t ) = x x + y x + y + z x + y + z + t . Show that f is surjective.
Matrices as symbolic representations of linear transformations
Matrices are the conventional concrete representation we adopt for linear transformations between vector spaces that can be represented symbolically using the usual vector and span notation (i.e., subspaces of Rn). Thus, we can interpret any matrix M ∈ Rn → Rm as the linear transformation f: Rm → Rn with the definition f(v) = M ⋅ v.
Fact: For any matrix M ∈ Rn×m, the map f: Rm → Rn defined as f(v) = M ⋅ v is a linear transformation.
Fact: The image of the linear transformation f(v) = M ⋅ v represented by M ∈ Rn×m is the span of the column vectors of M. Let w1,...,wn be the columns of M. We can see this by noting that
f( a1 ⋮ an ) = M ⋅ a1 ⋮ an = a1 w1 + ... + an wn. Fact: The image of the linear transformation represented by M ∈ Rn×m is a vector space (and a subspace of Rm). Why is this?
Fact: If a matrix M ∈ Rn×n is invertible and f(v) = M ⋅ v, then f is injective.
Fact: If a matrix M ∈ Rn×n is invertible and f(v) = M ⋅ v, then ker f = {0}.
Fact: For a matrix M ∈ Rn×n and f(v) = M ⋅ v where ker f = {0}, then M is invertible.
Fact: If a matrix M ∈ Rn×n represents a linear transformation f(v) = M ⋅ v and ker f = {0}, then the system M v = 0 has exactly one solution.
Review #2
This section contains a comprehensive collection of review problems going over all the course material covered until this point. These problems are an accurate representation of the kinds of problems you may see on an exam.
Problem: Given u ∈ Rn, what is the orthogonal projection of v ∈ Rn onto span{u}?
It is sufficient to compute the orthogonal projection of v onto u. Given a unit vector e parallel to u, the projection of v onto e would be:(e ⋅ v) ⋅ e.However, we cannot assume u is a unit vector. Thus, we scale u to obtain a unit vector e = u/||u||. Then, the solution is:
((u/||u||) ⋅ v) ⋅ (u/||u||).Problem: Assume a matrix M ∈ R2×2 is symmetric, has constant diagonal, and all its entries are nonzero. Show that A cannot be an orthogonal matrix.
Let a ≠ 0 and b ≠ 0, and let us define:M = a b b a . Suppose that M is an orthogonal matrix; then, we have that:
M -1 = M⊤ M ⋅ M⊤ = I a b b a ⋅ a b b a = 1 0 0 1 . Thus, we have ba + ab = 0, so 2ab = 0. This implies that either a = 0 or b = 0. But this contradicts the assumptions, so M cannot be orthogonal.
Problem: Let M ∈ R17× 9 and f(v) = M ⋅ v. What is the largest possible value of dim(im(f))?
We know that we can only compute M v if v has as many rows as M has columns. Thus, if f(v) = M ⋅ v, then v ∈ R9. We also know that M ⋅ v will be a vector with 17 rows because M has 17 rows, so f(v) ∈ R17. Thus, f ∈ R9 → R17.This means that dim(im(f)) cannot be greater than dim(R17), so it cannot exceed 17. However, we also need to note that M has 9 columns, and that any value in the image of f is thus a linear combination of at most 9 vectors. Thus, any basis of im(f) has at most 9 distinct vectors in it. Since dim(im(f)) is the size of the basis of im(f), dim(im(f)) can be at most 9.
Problem: Find an orthonormal basis for the following vector space:
span { 1 0 2 0 , 0 1 2 3 , 0 0 0 1 }. We can use the algorithm for computing the vectors in an orthonormal basis. We can work with the vectors in any order, so suppose we have:v1 = 0 0 0 1 , v2 = 0 1 2 3 , and v3 = 1 0 2 0 . According to the algorithm, we then let u1 = v1 and e1 = u1 / ||u1||. In this case, we still have e1 = v1. Next, we compute:
u2 = v2 - ((v2 ⋅ e1) ⋅ e1) = 0 1 2 3 - 0 0 0 3 = 0 1 2 0 e2 = 0 1/√(5) 2/√(5) 0 u3 = v3 - ((v3 ⋅ e1) ⋅ e1) - ((v3 ⋅ e2) ⋅ e2) = 1 0 2 0 - 0 0 0 0 - 0 4/5 8/5 0 = 1 -4/5 2/5 0 e3 = (3√(5))/5 ⋅ 1 -4/5 2/5 0 Thus, {e1, e2, e3} is an orthonormal basis for span{v1, v2, v3}.
Problem: Suppose we are given a linear transformation f:R2 → R2 where:
f(v) = 2 7 3 1 ⋅ v. - Find an orthonormal basis for im(f).
- Find ker(f).
- Show that f is surjective.
We know that the column vectors of the matrix are linearly independent. Thus, dim(im(f)) as at least 2, and since the codomain of f is R2, im(f) = R2. Thus, any orthonormal basis of R2 is appropriate, such as:{ 1 0 , 0 1 }. Let the matrix in the definition of f be M. We know from lecture that M is invertible iff ker(f) = {0}. Since det M ≠ 0, M is invertible, so ker(f) = {0}.Alternatively, we could recall the definition of a kernel:
ker(f) = {v | f(v) = 0}. Thus, it is sufficient to find the set of solutions to the equation f(v) = 0, which is the set of solutions (expanding the definition of f) of:
2 7 3 1 ⋅ v = 0 0 . Since M is invertible, we can multiply both sides by M -1 to obtain:
v = 1/(3-21) ⋅ 1 -7 -3 2 ⋅ 0 0 v = 0 0 . Thus, there is only one solution, so the kernel contains a single element, and ker(f) = {0}.
To show that f is surjective, it is sufficient to show that for every v in the codomain, there exists x such that:f(x) = v. In other words, we want a formula for x in terms of v that is defined for any v. Let the matrix in the definition of f be M. Since M is invertible, we can define:
x = 1/(3-21) ⋅ 1 -7 -3 2 ⋅ v This formula for x is always defined, so f is surjective.
Problem: Suppose we are given a linear transformation f:R2 → R2 where:
f(v) = 2 1 8 4 ⋅ v. - Find dim(im(f)).
- Show that f is not injective.
- Find ker(f).
Recall that the dimension of a space is the size of any basis of that space (all bases of a space have the same size). Let M be the matrix in the definition of f. The space im(f) is equivalent to the span of the column vectors of the matrix:im(f) = span{ 2 8 , 1 4 } To find a basis of a space spanned by a collection of vectors, we create a matrix whose rows are the vectors in that collection, find its reduced row echelon form, and keep only the nonzero rows in the basis:
2 8 1 4 → 1 4 1 4 → 1 4 0 0 im(f) = span{ 1 4 } Thus, the dimension of im(f) is 1.
To show that a map is not injective, it is sufficient to find v and v' such that v ≠ v' but f(v) = f(v').One approach to finding such v and v' is to expand f(v) = f(v') until the constraints are simple enough that it is straightforward to try some inputs and easily check that they satisfy the constraints.
f(x) = f(x') 2 1 8 4 ⋅ x y = 2 1 8 4 ⋅ x' y' Since the top row of the matrix is a multiple of the bottom row, we get one equation:
x ≠ x' y ≠ y' 2x + y = 2x' + y' One possible pair of vectors in the domain that satisfies the above is:
x y = 0 2 x' y' = 1 0 Thus, f is not injective.
We write down the definition of ker(f) for this particular map f:ker(f) = { x y | f( x y ) = 0 0 } = { x y | 2 1 8 4 ⋅ x y = 0 0 } The above would be sufficient, but suppose we want to find the basis of ker(f) (recall that ker(f) is a subspace of the domain of the linear transformation f). The constraints imposed above can be summarized as:
ker(f) = { x y | 2x + y = 0} = { x y | y = -2x} Thus, ker(f) is the line in R2 defined by the equation y = -2x. We can choose any vector on this line and take the span of the set containing only that vector to provide an explicit definition for ker(f):
ker(f) = span { -1 2 } . Problem: Find a matrix M such that for f(v) = M ⋅ v,
im(f) = (span{ 2 0 0 0 , 0 0 2 0 })⊥ One way to approach this problem is to expand the definition on the right-hand side using the definition of the orthogonal complement operation:im(f) = (span{ 2 0 0 0 , 0 0 2 0 })⊥ = { x y z t | 2 0 0 0 ⋅ x y z t = 0, 0 0 2 0 ⋅ x y z t = 0 } = { x y z t | 2x = 0, 2z = 0, y,t ∈ R } = { x y z t | x = 0, z = 0, y,t ∈ R } = { 0 y 0 t | y,t ∈ R }. Thus,
im(f) = span{ 0 1 0 0 , 0 0 0 1 }. Recall that the image of f is the span of the columns of M. Thus, one possible solution is:
M = 0 0 1 0 0 0 0 1 . Problem: Suppose that a2 + b2 = 1. What is the orthogonal projection of v onto im(f) if f(v) = M ⋅ v,
v = 1 2 3 , and M = a 0 0 b 0 0 0 c 0 . We have that:im(f) = span{ a b 0 , 0 0 c }. Because a2 + b2 = 1, the first vector is already a unit vector and orthogonal to the second vector. By rescaling the second vector to be a unit vector, we can obtain an orthonormal basis:
im(f) = span{ a b 0 , 0 0 1 }. We can now find the orthogonal projection of v onto each vector in the orthonormal basis, and add these to find the orthogonal projection of the vector onto im(f):
( 1 2 3 ⋅ a b 0 ) ⋅ a b 0 + ( 1 2 3 ⋅ 0 0 1 ) ⋅ 0 0 1 = a2 + 2ba ab + 2b2 3 . Problem: Suppose we are given the following points:
0 6 , 2 6 , 2 12 . - Find a function of the form f(x) = ax2 + bx + c that is the best least-squares fit for these points.
We begin by writing down the equations in terms of f for each point:
f(0) = 6 f(2) = 6 f(2) = 12 We construct the matrix equation that represents the above system:
(0)2 (0) 1 (2)2 (2) 1 (2)2 (2) 1 ⋅ a b c = 6 6 12 There is no solution to the above equation. However, we are looking for the least-squares best fit approximation. Thus, we first find an orthonormal basis of the image of the matrix. If the matrix is M and f(v) = M ⋅ v, we have that:
im(f) = span { 0 4 4 , 0 2 2 , 1 1 1 }. Using the algorithm for finding an orthonormal basis, we obtain:
im(f) = span { 0 1/√{2} 1/√{2} , 1 0 0 }. We now find the orthogonal projection of 6 6 12 onto im(f) and use it to rewrite the equation so that it is not overdetermined: (0)2 (0) 1 (2)2 (2) 1 (2)2 (2) 1 ⋅ a b c = 6 9 9 This system is underdetermined. The space of solutions implied by the above equation is:
{ f | f(x) = ax2 + bx + c, c = 6, 4a + 2b + c = 9} This means that any solution to the system is a least-squares best fit approximation. One possible best fit approximation is:
f(x) = x2 + (-1/2)x + 6 - Find a function of the form f(x) = bx + c that is the best least-squares fit for these points.
We follow the same process as in part (a) above. The matrix equation is:
(0) 1 (2) 1 (2) 1 ⋅ b c = 6 6 12 There is no solution to the above equation. However, we are looking for the least-squares best fit approximation. Thus, we first find an orthonormal basis of the image of the matrix. If the matrix is M and f(v) = M ⋅ v, we have that:
im(f) = span { 0 2 2 , 1 1 1 }. Using the algorithm for finding an orthonormal basis, we obtain:
im(f) = span { 0 1/√{2} 1/√{2} , 1 0 0 }. We again find the orthogonal projection of 6 6 12 onto im(f) and use it to rewrite the equation so that it is not overdetermined: (0) 1 (2) 1 (2) 1 ⋅ b c = 6 9 9 This yields c = 6 and b = 3/2. Thus, the least-squares best fit approximation is:
f(x) = (3/2)x + 6
Problem: Show that for M ∈ Rn×n, the space of solutions to M x = 0 is a vector space (you do not need to show that all the axioms hold; it is sufficient to show the appropriate closure properties).
Let S be the space of solutions.We show that 0 ∈ S:
M ⋅ 0 = 0. We show that if v,v' ∈ S, then v + v' ∈ S:
M ⋅ v = 0 M ⋅ v' = 0 M ⋅ (v + v') = M ⋅ v + M ⋅ v' = 0 + 0 = 0. We show that if v ∈ S, then for any scalar s ∈ R, s v ∈ S:
M ⋅ v = 0 M ⋅ (s ⋅ v) = s ⋅ (M ⋅ v) = s ⋅ 0 = 0. Problem: Compute the orthogonal projection of v onto im(f) where f(v) = M ⋅ v,
v = 1 -2 3 , and M = 1 1 2 8 1 5 . Normally, the way to approach such problems is to find an orthonormal basis for im(f) where f(v) = M ⋅ v, then use that orthonormal basis to project v onto im(f). However, it's a good idea to check for special cases before delving into a large computation. In this particular example, we have that:1 -2 3 ⋅ 1 2 1 = 0 1 -2 3 ⋅ 1 8 5 = 0. Thus, v is orthogonal to both vectors, so the orthogonal projection of v onto im(f) is 0 ∈ R3.
It is worth noting that v is in the orthogonal complement of im(f). In general, given a vector subspace W ⊂ V, for any w ∈ W⊥, the orthogonal projection of w onto W is 0.
Problem: Is the system below overdetermined or underdetermined? Does it have a solution?
1 2 0 0 1 -4 0 0 1 ⋅ v = 8 3 0 . The system is neither overdetermined nor underdetermined. It has a solution. Since the matrix is upper triangular, we can use the algorithm for solving a system with an upper triangular matrix to obtain v:v = 2 3 0 . Problem: Determine whether the system below has a solution for all possible v ∈ R3. If it does not, describe exactly the set of vectors v for which the system below has a solution and determine whether this set a vector space.
1 2 2 0 2 -1 1 4 1 ⋅ x = v . Notice that determining whether the system has a solution for any v is equivalent to determining whether the linear transformation represented by the matrix is surjective. It is also equivalent to determining whether the matrix is invertible.To determine whether the matrix is invertible, we could compute its reduced row echelon form by finding an appropriate series of row operations.
1 2 2 0 2 -1 1 4 1 → 1 2 2 0 1 -1/2 1 4 1 → 1 0 3 0 1 -1/2 1 4 1 → 1 0 3 0 1 -1/2 0 4 -2 → 1 0 3 0 1 -1/2 0 0 0 Given the above, we see that the matrix is not invertible.
Let the matrix be M. The set of vectors for which there is a solution to the above equation is im(f) where f(x) = M ⋅ x. Thus, we want to find im(f) explicitly. We could say:
im(f) = span { 1 0 1 , 2 2 4 , 2 -1 1 }. If we want to be more precise, we could compute rref(M⊤) to find a basis for im(f).
Since the set of possible vectors v for which the equation has a solution is im(f) and f is a linear transformation, the set of such v is a vector space.
Assignment #4: Algebra of Linear TransformationsIn this assignment you will work with vector spaces and linear transformations.
- Complete the following argument.
∀ f,g ∈ R2 → R2, ∀ x,y ∈ R2,
(f o g) is bijective and
x ≠ y
implies
# ...
(g o f)(x) ≠ (g o f)(y)
- Complete the following argument.
∀ f ∈ R2 → R2,
( 1 2 3 4 ) represents (f)
implies
# ...
(f) is bijective - Complete the following argument.
∀ f,g ∈ R2 → R2,
( 1 2 3 6 ) represents (f) and ( 2 4 -1 -2 ) represents (g)
implies
# ...
img(g) ⊂ ker(f)
- Complete the following argument.
∀ f ∈ R2 → R2,
( 4 7 2 5 ) represents (f)
implies
# ...
(f) is surjective
Orthogonal Projections are Linear Transformations
Fact: For v ∈ Rn, an orthogonal projection onto a one-dimensional vector space span{v} is a linear transformation. First, note that the dot product of two vectors can be rewritten as matrix multiplication of two matrices:
u ⋅ v = u⊤ ⋅ v.Also, notice that
||v|| = √(v ⋅ v) ||v||2 = v ⋅ v Finally, notice that for nonzero r ∈ R where r ≠ 0, the matrix
r is invertible and has inverse 1/r . Consider the formula for the projection of w ∈ Rn onto span(v). We can rewrite the formula to use only multiplication of matrices.
(v/||v|| ⋅ w) ⋅ v/||v|| = 1/||v||2 ⋅ (v ⋅ w) ⋅ v = v ⋅ 1/||v||2 ⋅ (v ⋅ w) = v ⋅ 1/(v ⋅ v) ⋅ (v ⋅ w) = v ⋅ (v⊤ ⋅ v) -1 ⋅ (v⊤ ⋅ w) = (v ⋅ (v⊤ ⋅ v) -1 ⋅ v⊤) ⋅ w Thus, we have a product of the matrices v ∈ Rn×1, (v⊤ ⋅ v) -1 ∈ R1×1, and v⊤ ∈ R1×n. This product is a matrix in Rn×n. Call it Mspan{v}. Then we can define the linear transformation f ∈ Rn → Rn that performs the orthogonal onto span{v} as:
f(w) = Mspan{v} ⋅ w.We used the above approach because we will see later that it can be generalized to orthogonal projections onto multidimensional vector spaces. An alternative way to show the above is to notice that v/||v|| can be rewritten as a matrix u ∈ Rn×1. In that case, we have:
(v/||v|| ⋅ w) ⋅ v/||v|| = (u ⋅ w) ⋅ u = u ⋅ (u ⋅ w) = (u ⋅ u⊤) ⋅ w Here, u ⋅ u⊤ ∈ Rn×n.
Fact: Any orthogonal projection onto a subspace span{v1,...,vm} ⊂ Rn is a linear transformations. We know that we can find an orthonormal basis of span{v1,...,vm}. Let M be a matrix the columns of which form an orthonormal basis of span{v1,...,vm}. Then, we can define f ∈ Rn → Rn as:
f(w) = M ⋅ M⊤ ⋅ w.In fact, by generalizing the formula for projections onto a one-dimensional subspace, we can in certain cases avoid relying on our ability to compute an orthonormal basis for span{v1,...,vm}. However, before we can derive the generalized formula, we need a few preliminary results.
Example: Consider the case where we have
w = 1 2 3 M = 1 2 3 f(v) = M ⋅ v g(v) = M⊤ ⋅ v. Let V = im(f). Then V⊥ is the set of vectors orthogonal to w. A vector u ∈ R3 is orthogonal to w iff w ⋅ v = 0. But this means M⊤ ⋅ w = 0, which means w ∈ ker(g).
Fact: Take any matrix M ∈ Rn×m and linear transformations f ∈ Rm → Rn and g ∈ Rn → Rm defined as
f(v) = M ⋅ v g(v) = M⊤ ⋅ v. We have that
im(f)⊥ = ker(g).To show these two sets are equal, we can make two arguments:
im(f)⊥ ⊂ ker(g) ker(g) ⊂ im(f)⊥. ∀ f,g ∈ R2 → R2, ∀ M ∈ R2×2, ∀ v ∈ R2,
(M) represents (f) and
(M⊤) represents (g) and
v ∈ ker(g)
implies
g(v) = 0 0 and g(v) = M⊤ ⋅ v and M⊤ ⋅ v = 0 0 and v ∈ (im(f))⊥
∀ f,g ∈ R2 → R2, ∀ M ∈ R2×2, ∀ v ∈ R2,
(M) represents (f) and
(M⊤) represents (g) and
v ∈ (im(f))⊥
implies
M⊤ ⋅ v = 0 0 and g(v) = M⊤ ⋅ v and g(v) = 0 0 and v ∈ ker(g)
Because the subset relation applies to the two sets in both directions, the two sets must be equal.
Fact: We show that if a vector is in the kernel of a linear transformation f ∈ Rn → Rm, for any g ∈ Rm → Rk, it is also in the kernel of the linear transformation g o f. In other words, ker(f) ⊂ ker(g o f).
∀ f,g ∈ R2 → R2, ∀ A,B ∈ R2×2, ∀ v ∈ R2,
(A) represents (f) and
(B) represents (g) and
v ∈ ker(f)
implies
#...
v ∈ ker(g o f)Fact: Let M ∈ Rn×m and f,g ∈ Rm → Rn be defined as
f(v) = M ⋅ v g(v) = M⊤ ⋅ v. We have that:
ker(f) = ker(g o f).We know that ker(f) ⊂ ker(g o f) from the previous fact. It suffices to show that
ker(g o f) ⊂ ker(f).The argument below does just that. Notice that we use the fact that ker(g) = im(f)⊥ (for appropriate f and g) that we derived above.
∀ f,g ∈ R2 → R2, ∀ M ∈ R2×2, ∀ v ∈ R2,
(M) represents (f) and
(M⊤) represents (g) and
v ∈ ker(g o f)
implies
(g o f)(v) = 0 0 and (g o f)(v) = g(f(v)) and g(f(v)) = 0 0 and g(f(v)) = M⊤ ⋅ f(v) and f(v) = M⋅v and (g o f)(v) = M⊤ ⋅ (M ⋅ v) and M⊤ ⋅ (M ⋅ v) = 0 0 and g(M⋅v) = 0 0 and (M⋅v) ∈ ker(g) and M⋅v ∈ im(f) and ker(g) = (im(f))⊥ and M⋅v ∈ (im(f))⊥ and M⋅v = 0 0 and f(v) = 0 0 and v ∈ ker(f)
Fact: Suppose that for M ∈ Rn×m and f ∈ Rm → Rn where f(x) = M ⋅ x we have an overdetermined system:
M ⋅ x = v.Suppose that ker(f) = {0}. Then for g ∈ Rn → Rm where g(y) = M⊤ ⋅ y, we have that
ker(g o f) = ker(f) = {0}.Then we have that g o f is invertible, so M⊤ ⋅ M is invertible and (M⊤ ⋅ M) -1 is defined. Thus, we can say that
M⊤ ⋅ (M ⋅ x) = M⊤ ⋅ v (M⊤ ⋅ M) ⋅ x = M⊤ ⋅ v (M⊤ ⋅ M) -1 ⋅ (M⊤ ⋅ M) ⋅ x = (M⊤ ⋅ M) -1 M⊤ ⋅ v x = (M⊤ ⋅ M) -1 M⊤ ⋅ v M ⋅ x = M ⋅ (M⊤ ⋅ M) -1 M⊤ ⋅ v. Thus, even if M ⋅ x = v is overdetermined, M⊤ ⋅ (M ⋅ x) = M⊤ ⋅ v has a solution x such that M ⋅ x corresponds to the projection of v onto im(f).
Fact: If a matrix M ∈ Rn×m represents a linear transformation f(v) = M ⋅ v, then we have that
dim(im(f)) = rank(M).Fact (Rank-Nullity Theorem): If a matrix M ∈ Rn×m represents a linear transformation f(v) = M ⋅ v, then we have that
dim(ker(f)) + dim(im(f)) = n.There is more than one way to understand the above.
Applications to Linear Systems
Interpreting and Using Vector Spaces and Linear Transformations in Applications
Let V,W ⊂ Rn be vector spaces, and let f: V → W be a linear transformations. The following table reviews the operators we introduced for working with sets of vectors, vector spaces, and linear transformations.
operator input output additional properties span V set of vectors vector space basis V vector space set of vectors the output is finite if
the V has finite dimension
(since dim V = |basis V|)dim V vector space integer V⊥ vector space vector space im f linear transformation vector space subspace of the codomain W ker f linear transformation vector space subspace of the domain V In this section, we consider how these operators and their properties are interpreted within particular applications, and how they can be used to represent and solve problems within these application domains.
Example: Suppose there are eight islands labelled A,B,C,D, and E,F,G,H, and the following adjacency matrix M ∈ R4× 4 represents whether bridges exist between pairs of islands:
E F G H A 1 bridges from A to E 0 bridges from A to F 0 bridges from A to G 0 bridges from A to H B 0 bridges from B to E 1 bridges from B to F 0 bridges from B to G 0 bridges from B to H C 0 bridges from C to E 1 bridges from C to F 0 bridges from C to G 1 bridges from C to H D 1 bridges from D to E 0 bridges from D to F 1 bridges from D to G 0 bridges from D to H We can extract information from this matrix by multiplying it by a vector in R4.
1 bridges from A to E 0 bridges from A to F 0 bridges from A to G 0 bridges from A to H 0 bridges from B to E 1 bridges from B to F 0 bridges from B to G 0 bridges from B to H 0 bridges from C to E 1 bridges from C to F 0 bridges from C to G 1 bridges from C to H 1 bridges from D to E 0 bridges from D to F 1 bridges from D to G 0 bridges from D to H ⋅ 1 count bridges to E 0 ignore bridges to F 1 count bridges to G 0 ignore bridges to H = 1 bridges from A to E or G 0 bridges from B to E or G 0 bridges from C to E or G 2 bridges from D to E or G Let f: R4 → R4 be defined as f(v) = M ⋅ v.
-
What is ker(f)? What does this mean about the connectedness of the islands?
Since ker(f) = {0}, there must be at least one bridge to every destination E,F,G, or H. In other words, if we choose to count bridges to even one destination in v, the product of M ⋅ v will be nonzero.
-
Suppose for some other adjacency matrix M' and g(v) = M' ⋅ v, we have that ker(g) ≠ {0}.
Does this necessarily imply that at least one island has no bridges going to it?
No. We could have 1 for all entries of M`, but the kernel would then have dimension 3 (and thus be nonzero). For example,we could let
Then, v ∈ ker(g) so ker(g) ≠ {0}, but all destination islands have a bridge going to them.v = 1 -1 0 0 . -
In terms of ker(f) and other sets and set operators, provide sufficient conditions such that M must describe a situation in which
each destination island has at least one bridge going to it.
It must be that ker(f) ∩ (R+)4 ≠ {0}.
Example: Suppose we have some noisy observations of a system (radiation at three wavelengths on a logarithmic scale and the quantity of particles observed). We have only sampled this system on four points:
IR UV γ quantity 1 -1 2 1 2 0 0 4 0 2 -4 2 3 1 -2 5 Suppose we believe that the quantity of particles is a linear function of the three radiation quantities. Find the least-squares approximation of a linear relationship between the three dimensions describing the radiation output and the quantity of particles.
One way to use our existing technique for finding approximate functions that fit data is to imagine that there are three unknown functions (e.g., polynomials) p,q,r ∈ R → R whose inputs are defined to be the observations. Then, we are looking for a linear combination of these,f(x) = a ⋅ p(x) + b ⋅ q(x) + c ⋅ r(x),that best approximates the data:
IR UV γ quantity p(0) = 1 q(0) = -1 r(0) = 2 f(0) = a ⋅ p(0) + b ⋅ q(0) + c ⋅ r(0) = 1 p(1) = 2 q(1) = 0 r(1) = 0 f(1) = a ⋅ p(1) + b ⋅ q(1) + c ⋅ r(1) = 4 p(2) = 0 q(2) = 2 r(2) = -4 f(2) = a ⋅ p(2) + b ⋅ q(2) + c ⋅ r(2) = 2 p(3) = 3 q(3) = 1 r(3) = -2 f(3) = a ⋅ p(3) + b ⋅ q(3) + c ⋅ r(3) = 5 Notice that this is just a generalization of our approach to modelling data points using polynomials: in those cases, we might have had p(x) = x2, q(x) = x, r(x) = 1.
We can also view this problem as a search for a linear transformation g:R3 → R that will be a least-squares approximation of the data; it can be defined as:
g( x y z ) = a b c ⋅ x y z In a manner similar to previous examples, we can represent the problem as a matrix of inputs and a vector of dependent outputs (one row per data point):
M = 1 -1 2 2 0 0 0 2 -4 3 1 -2 , v = 1 4 2 5 . Thus, we want a least-squares approximate solution to the overdetermined system:
1 -1 2 2 0 0 0 2 -4 3 1 -2 ⋅ u = 1 4 2 5 . Let h,h' ∈ R3 → R4 be defined as h(u) = M ⋅ u and h'(u) = M⊤ ⋅ u. We can find the approximation for the above overdetermined system by first finding the orthogonal projection of v onto im(h). However, We cannot directly use the formula u = (M⊤ ⋅ M) -1 M⊤ v because ker(h) ≠ {0}:
1 -1 2 2 0 0 0 2 -4 3 1 -2 ⋅ a b c = 0 0 0 0 2 a = 0 2 b - 4 c = 0 a - b + 2 c = 0 a = 0 b = 2 c = -1 1 -1 2 2 0 0 0 2 -4 3 1 -2 ⋅ 0 2 -1 = 0 0 0 0 0 2 -1 ∈ ker(h) ker(h) ≠ {0} This means ker(h' o h) ≠ {0}. This means M⊤ ⋅ M is not invertible, so (M⊤ ⋅ M) -1 is undefined.
If the matrix of data observations M has a nonzero kernel, it must have at least one column vector that is a linear combination of the other column vectors. But within the context of the problem this means that for any data point, the value of the dependent dimension can be determined using the values along the other dimensions. Thus, we need not include this dimension explicitly in our attempt to model the observations.
The above calculation indicates that the third column vector is a scalar multiple of the second column vector. Suppose we remove the third column vector from our data. Then, we have:
N = 1 -1 2 0 0 2 3 1 , l(u) = N ⋅ u, l'(u) = N⊤ ⋅ u. Thus, we can instead look for an approximate solution to the following system:
1 -1 2 0 0 2 3 1 ⋅ a b = 1 4 2 5 . This system is overdetermined. However, we have:
1 -1 2 0 0 2 3 1 ⋅ a b = 0 0 0 0 2 a = 0 2 b = 0 ker(l) = { a b | a = 0, b = 0} = { 0 0 } ker(l) = {0} Thus, ker(l' o l) = {0}, which means (N⊤ ⋅ N) -1 is defined. We can then compute our approximation using the closed formula:
u* = (N⊤ ⋅ N) -1 ⋅ N⊤ ⋅ v = ( 14 2 2 6 ) -1 ⋅ 1 2 0 3 -1 0 2 1 ⋅ 1 4 2 5 = (1/80) 6 -2 -2 14 ⋅ 1 2 0 3 -1 0 2 1 ⋅ 1 4 2 5 Communications: Applications of Curve Approximations and Properties of Linear Transformations
Example: Suppose that Alice wants to transmit some data to Bob, and this data consists of the following table:
T := 3 -1 5 10 7 -7 3 0 -15 7 0 2 4 14 -2 14 7 -35 5 2 0 0 8 4 16 11 -25 2 1 3 6 3 -1 7 5 -10 0 4 -1 -2 -4 9 12 12 0 Since T ∈ R5× 9, the straightforward solution would be to transmit 5 ⋅ 9 = 40 scalar values. However, it is not necessary to transmit all five scalar values found in every column.
- Devise a different approach for sending such data that requires sending fewer than 40 scalar values for the above example; the approach should be such that if Alice and Bob can agree on how it works, they can reliably transmit all the data.
- Suppose the matrix of data to transmit is T ∈ Rm×n. Using the dim and im operators, write a formula describing exactly how many scalar values will need to be sent in order to transmit all the data in T using the method you devised.
Example: Suppose that Alice wants to transmit some data (a sequence of numbers) to Bob without revealing what they are to Eve, who can read anything Alice sends. One simple encryption scheme involves splitting the message into vectors v ∈ Rn and using a matrix M ∈ Rn×n to convert them into something that would be unrecognizable to an eavesdropper. For example, suppose the message is:
1, 2, 3, 4Alice could split the above message into two vector in R2:
1 2 , 3 4 She could then use a matrix M to convert these into something unrecognizable:
3 1 2 1 1 2 , 3 1 2 1 3 4 This yields the following vectors, which Alice then transmits to Bob:
5 4 , 13 10 -
If Alice sends a message to Bob using the above method, how can Bob decode the message?
Bob can compute the inverse of the encoding matrix and apply it to the messages he receives.
-
Suppose Eve finds out what matrix Alice and Bob are using. If Alice and Bob choose a new matrix, what conditions must
be satisfied by the matrix (or the corresponding linear transformation) that Alice will use to encode her messages?
The matrix and corresponding linear transformation must be invertible in order for Bob to be able to recover the message in full.
-
Suppose that Eve does not know M, but does know at least one sequence of two consecutive numbers
that were encoded using the matrix (for example, suppose Eve knows that every morning Alice sends a message telling Bob whether it is
sunny (unencoded sequence 1,2) or cloudy (unencoded sequence 3,4) at her location). Show that if Eve is near Alice's location, Eve
will eventually be able to decode any message Alice sends using that matrix.
Once Eve has seen an encoded message for both a sunny day and a cloudy day, she can solve the following system to obtain the components of the matrix:
a b c d 1 2 = 5 4 a b c d 1 2 = 13 10 -
Let s be the unencoded vector Alice uses to represent a sunny day, let c be the unencoded vector she uses to represent a cloudy day,
and let f be the linear transformation she uses to encode her messages. Provide sufficient conditions on s and c such that Eve will
not be able to recover the entire matrix M using the method in part (c) above; express you conditions in terms of s, c, and f by using im
and span.
It must be that span{s,c} = im(f).
Example: More generally, a flaw with Alice's approach is that Eve can detect when Alice sends the same message twice. This leaks information to Eve about the content of her messages (for example, if Alice is encoding English sentences, the most commonly occurring letter in those sentences will be "e").
In order to address this, Alice can extend her encoding process. She can take all her vectors in R2 and convert them into vectors in R3, and then use a matrix in R3 to encode them:E = 3 1 2 1 0 0 Bob could then decode any such message using the following matrix (notice that the top-left 2 × 2 portion of this matrix is the inverse of the top-left 2 × 2 portion of the matrix above):
1 -1 0 -2 3 0 0 0 0 In fact, Bob can decode the messages using any matrix of the form:
D = 1 -1 a -2 3 b 0 0 c Let g(v) = D ⋅ v. Then, because g is a linear transformation, for any w ∈ ker(g) we have that:
g(v + w) = g(v) + g(w) = g(v) + 0 But this means that Alice can take each encoded vector E ⋅ v that she creates and add any w ∈ ker(g) to it in order to obfuscate any patterns that Eve might see in the encoded messages. Alice can choose a random w ∈ ker(g) for each message. Bob will easily be able to continue decoding Alice's messages using the same transformation g.
- Suppose Alice has a random vector generator that takes as an input a matrix M ∈ R3× 3 and returns a random vector in im(h)⊥ where h(v) = M ⋅ v. How can she use this generator to create obfuscated encrypted message vectors?
- If Alice wants to hide any patterns in the messages she sends over time (including any patterns in parts of her messages), what is a necessary property of ker(g)?
-
Given an encoding matrix E ∈ R3×2, how can Alice and Bob find D such that ker(g) ≠ {0} and such that the
desired property from part (b) above holds?
Let the column vectors of D be d1, d2, and d3. What is needed is a vector d3 that satisfies the following:d3 ∈ (span {d1, d2} - span {d1} - span {d2})
-
Suppose Alice has a random number generator that can only generate a single scalar r ∈ R at any given moment.
Find a single matrix E' ∈ R3× 3 that Alice can use to convert message vectors with a random number, of the following form:
v = x y r so that E' ⋅ v is always an obfuscated encrypted message vector.
Example: Suppose Alice has an unreliable communication device that can transmit any vector v ∈ R2 to Bob, but will always add an error vector e to v where ||e|| is bounded by 5:
v ↦ v + e ||e|| < 5 Find two matrices A and B such that if Alice wants to send v to Bob, she can send A ⋅ v using the device and after receiving the transmission (call it w), Bob can always recover a close approximation B ⋅ w that has at most error 0.25 (that is, ||B ⋅ w - v|| ≤ 0.25).
It is sufficient to scale the vector being sent to make the error negligible, and then to scale it back down once it is received. Thus,A = 100 0 0 100 B = 0.01 0 0 0.01 Then, we have for any v being sent:
A v ↦ (100 ⋅ v) + e When Bob decodes it, it will be:
B (A v + e) = 0.01 ((100 ⋅ v) + e) = v + 0.01 e Then we have in the worst case ||e|| = 5, which means:
|| 0.01 ⋅ e || = 0.01 ⋅ ||e|| = 0.05 Example: Alice has two unreliable communication devices for transmitting vectors in R2. Given a vector v ∈ R to transmit, the first device will add an arbitrarily large error vector during transmission (ε varies between transmissions):
v ↦ v + ε ⋅ 1 2 The second device will add a different arbitrarily large error vector during transmission:
v ↦ v + ε' ⋅ 6 -3 Alice wants to send a vector v ∈ R2 to Bob by sending only two messages, one with each device. Devise a way for Alice to send v ∈ R2 in this way so that Bob can recover it without any error. This method should not rely in any way on ε, and should work for any ε.
We can observe that the two error vectors are orthogonal. This means that each device can be used to reliably transfer the projection of a vector onto the orthogonal complement of the span of the error vector for that device. That is,projection of v onto (span { 1 2 })⊥ = projection of v + ε ⋅ 1 2 onto (span { 1 2 })⊥ projection of v onto (span { 6 -3 })⊥ = projection of v + ε' ⋅ 6 -3 onto (span { 6 -3 })⊥ Notice that because the two vectors are orthogonal complements, we have:
(span { 6 -3 })⊥ = span { 1 2 } (span { 1 2 })⊥ = span { 6 -3 } Thus, we can rewrite our first set of equalities:
projection of v onto span { 6 -3 } = projection of v + ε ⋅ 1 2 onto span { 6 -3 } projection of v onto span { 1 2 } = projection of v + ε' ⋅ 6 -3 onto span { 1 2 } We can now show that the above is true because, as we have seen further above, projection onto a vector space (including the span of a single vector) is a linear transformation. Suppose we define the following two projections:
p(v) = ( 6 -3 ⋅ ( 6 -3 ⊤ ⋅ 6 -3 ) -1 ⋅ 6 -3 ]⊤) ⋅ v q(v) = ( 1 2 ⋅ ( 1 2 ⊤ ⋅ 1 2 ) -1 ⋅ 1 2 ⊤) ⋅ v Thus, we have that:
p(v + ε ⋅ 1 2 ) = p(v) + ε ⋅ p( 1 2 ) = p(v) + ε ⋅ ((( 6 -3 ⋅ ( 6 -3 ⊤ ⋅ 6 -3 ) -1 ⋅ 6 -3 ]⊤) ⋅ 1 2 ) = p(v) + ε ⋅ ( 6 -3 ⋅ ( 6 -3 ⊤ ⋅ 6 -3 ) -1 0 ) = p(v) + ε ⋅ 0 0 = p(v) q(v + ε ⋅ 6 -3 ) = q(v) + ε ⋅ q( 6 -3 ) = q(v) + ε ⋅ 0 0 = q(v) Thus, Alice can simply use both devices to send v to Bob. When Bob receives w1 (from the first device) and w2 (from the second device), he must interpret them appropriately:
w1 = v + ε ⋅ 1 2 w2 = v + ε ⋅ 6 -3 Using our equalities from above, we have that:
projection of v onto span { 6 -3 } = projection of w1 onto span { 6 -3 } projection of v onto span { 1 2 } = projection of w2 onto span { 1 2 } p(v) = p(w1) q(v) = q(w2) Thus, to retrieve the original v sent by Alice it is sufficient for Bob to perform the two projections and to add the results:
v = p(v) + q(v) = p(w1) + q(w2) Example: Let polynomials in F = {f | f(t) = a t4 + b t3 + c t2 + d t + e } represent a space of possible radio signals. To send some information to Bob, Alice must use that information to generate a radio signal that is described by some f. To receive that information, Bob must listen to the radio signals he is receiving, determine what f Alice chose, and decode the message.
Suppose that a given area is saturated with noise or signals (e.g., communication by others) that are linear combinations of the following three polynomials:
g1(t) = 4 t2 - 2 t + 1 g2(t) = - 4 t - 2 g3(t) = 2 t3 + 6 t + 3 Devise a communication method that Alice and Bob can use that would allow Alice to send vectors in R2 to Bob despite the interference from the noise.
First, let us consider the communication method in this environment when no noise is present. In such a scenario, Alice can choose a vector v ∈ R5 to transmit. For example:v = -2 -1 0 1 2 She then has a radio transmitter generate the signal corresponding to the polynomial whose coefficients are represented by v:
f(t) = -2 t4 - t3 + t + 2 To receive the message, Bob samples the signal at five different values of t:
f(0) = 2 f(1) = 0 f(2) = -12 f(3) = -184 f(4) = -570 In order to recover the message v, Bob must find the coefficients of the curve in F that fits the above points. Thus, it is sufficient to solve the following equation using any appropriate technique. Notice that the solution is the vector Alice v that was is sending to Bob.
0 0 0 0 1 1 1 1 1 1 16 8 4 2 1 81 27 9 3 1 256 64 16 4 1 ⋅ a b c d e = 2 0 -12 -184 -570 Next, suppose that noise is present in the environment. In this scenario, Alice will not be able to send a vector in R5 directly. This is because for any signal polynomial f that Alice generates, Bob will only be able to sample some linear combination of polynomials that includes both Alice's signal and the noise from the environment:
f(t) + s1 g1(t) + s2 g2(t) + s3 g3(t) However, she can first find two polynomials that are linearly independent from the polynomials g1, g2, and g3 that constitute the radio noise in the environment:
1 0 0 0 0 ∉ span{ 0 0 4 -2 1 , 0 0 0 -4 -2 , 0 2 0 6 3 } 0 0 0 1 2 ∉ span{ 0 0 4 -2 1 , 0 0 0 -4 -2 , 0 2 0 6 3 } Then, to send a vector v ∈ R2 to Bob, Alice simply takes the corresponding linear combination of the two vectors and transmits the signal corresponding to the polynomial whose coefficients correspond to the components of this linear combination:
x ⋅ 1 0 0 0 0 + y ⋅ 0 0 0 1 2 For example, suppose Alice wants to send the following vectors in R2:
1 2 Then she computes:
1 ⋅ 1 0 0 0 0 + 2 ⋅ 0 0 0 1 2 = 1 0 0 2 4 She then transmits:
f(t) = t^5 + 2 t + 4 The signal Bob hears is some linear combination of Alice's signal and the noise signals in the environment. For example, suppose he hears the following (note that Bob does not know s1, s2, and s3).
f(t) + s1 g1(t) + s2 g2(t) + s3 g3(t) For the purposes of this example, suppose that he hears the following (again, note that Bob does not know the coefficients):
f(t) + 1 ⋅ g1(t) + 2 ⋅ g2(t) + 0 ⋅ g3(t) In order to receive the message, Bob can now do the following.
- Bob samples the signal at 5 time points to obtain an equation.
f(0) = 1 f(1) = -2 f(2) = 33 f(3) = 256 f(4) = 1057 0 0 0 0 1 1 1 1 1 1 16 8 4 2 1 81 27 9 3 1 256 64 16 4 1 ⋅ a b c d e = 1 -2 33 256 1057 - Next, Bob can solve the above equation to obtain a vector corresponding to the polynomial that includes both noise and Alice's signal.
a b c d e = 1 0 4 -8 1 At this point, Bob knows that this is a linear combination:
1 0 4 -8 1 = x 1 0 0 0 0 + y 0 0 0 1 2 + s1 0 0 4 -2 1 + s2 0 0 0 -4 -2 + s3 0 2 0 6 3 - Remove the noise from that vector by multiplying it by a matrix with an appropriate kernel.
- Determine what linear combination of Alice's two chosen vectors constitute what remains to determine the vector Alice sent.
Alternatively, Bob can do the following:
- Sample the signal at 10 time points to obtain an equation.
- Solve the equation to obtain both the parameters of the polynomial and the linear combination of the vectors Alice sent and the noise vectors.
Example: Alice has an unreliable communication device for transmitting scalars in R: for every sequence of scalars she sends, e.g.:
(s1, ..., sn),up to half of the scalars will be lost during transmission (Bob will know which positions in the sequence have missing scalars, but he will not know what their quantities were). Alice wants to send Bob a vector v ∈ R2, but she cannot use naive methods of duplication to send it reliably. For example, simply sending many copies of v will not guarantee delivery of both components because up to half of the components may be dropped, and these may (albeit with low probability) all be copies of the first component of v.Devise a way for Alice to send a Bob a vector v ∈ R2 using her device so that Bob can recover it without error. Alice and Bob may coordinate ahead of time to agree on the parameters of the method.
We first illustrate the method they can use using an example. Before parting, Alice and Bob agree on a subspace of R2 and a finite set of vectors W from that subspace:
W = { 1 0 , 2 0 , 3 0 , 4 0 } W ⊂ span{ 1 0 } They also agree that the first element in this set will be the special vector used for decoding. Next, suppose Alice wants to send the following vector to Bob:
v = 1 2 Alice first computes the intersection of the orthogonal complement of the span of each vector in W with span{v}. In this case, we have:
span{v} = { x y | y = 2 x} Thus, the intersections of the points in W and span{v} would be:
{ 1 2 , 2 4 , 3 6 , 4 8 } Next, Alice projects these onto the orthogonal complement of the subspace she and Bob initially chose to obtain:
{ 0 2 , 0 4 , 0 6 , 0 8 } She can now discard the 0 entries and sends only the second components to Bob:
{2, 4, 6, 8}Bob can recover the original message using any two of the above scalars. For example, suppose Bob receives only 4 and 8. Bob knows that these were generated using the following vectors in W:
2 0 , 4 0 Thus, Bob knows two vector in span{v}:
2 4 , 4 8 To determine span{v}, Bob must simply determine the slope of the line through these two vector:
{ a( 4 8 - 2 4 ) + 2 4 | a ∈ R } = span{ 1 2 } Finally, Bob recalls that the first vector in W was the decoding vector. How now compute the intersection of that vector's span and span{v} to obtain the original v:
span{ 1 2 } ∩ span{ 1 0 } = { 1 2 } Example: Suppose Alice has a very unreliable communication device for transmitting scalars in R: for every sequence of scalars she sends, up to half of them are lost; those scalars that do arrive have a bounded error of at most 5. Devise a way for Alice to send vectors in R2 to Bob so that he can always recover the sent vectors with an error of at most 0.25.
Assignment #5: Applications: CommunicationIn this assignment you will use concepts from linear algebra to solve several problems in the application domain of communication.
- Alice wants to send Bob the matrix T below. However, she can only afford to send 30 scalars or fewer. Will she be able to send a message
from which Bob can recover all the information in the matrix?
T := 0 3 1 -4 -1 -8 0 -6 -2 8 2 16 1 0 -2 0 -2 -9 -2 0 4 0 4 18 3 -9 -9 12 -3 -3 -6 18 18 -24 6 6 -2 -6 2 8 6 34 4 12 -4 -16 -12 -68 3 -3 -7 4 -5 -19 -6 6 14 -8 10 38 numColumns := undefined # replace with a formula in terms of T numRows := undefined # replace with a formula in terms of T basisSize := undefined # replace with a formula in terms of T numScalarsToSend := undefined # replace with a formula that produces an integer numScalarsToSend ≤ 30 - You know that Alice is using a matrix M ∈ R2×2 to send encoded vectors in R2 to Bob. You also know that she will only
send vectors from the following set:
{ 3 0 , 1 2 , 4 4 , 0 1 , 0 -2 , 7 2 , 2 1 , 1 -1 , -2 2 } You observe two encoded messages as they are being transmitted:
{ 4 -6 , 2 11 } Determine which two unencoded vectors Alice sent, and then use them along with the encoded vectors and some matrix operations to provide a definition of the encoding matrix. You should be able to use
\augmentto accomplish this using a definition that fits on a single line.∀ v,w ∈ R2, ∀ a,b,c,d ∈ R,
v = \undefined and w = \undefined and a b c d = \undefined
implies
# ...
a b c d ⋅ v = 4 -6 and a b c d ⋅ w = 2 11
-
Alice wants to send Bob a vector v ∈ R2. She has an unreliable device that can transmit a vector in R2 to Bob, but it always adds
the following error to v during transmission (where s is unknown ahead of time, and different
each time):
v ↦ v + s ⋅ -1 1 Alice and Bob will agree on some u, M, and M' before parting. When sending a vector with x and y components, Alice will use the device to transmit two vectors: (x ⋅ u) and (y ⋅ u). Bob will receive w and w' as defined below, and will decode v by computing M w + M w'. Find u,M, and M' that make it possible to retrieve v, and complete the argument below. Hint: review the propositions available in the verification system that deal with matrices and vectors, as they may allow some algebraic manipulations to be more concise.
∀ x,y,s,s' ∈ R, ∀ u,v,w,w' ∈ R2, ∀ M,M' ∈ R2×2,
u = \undefined and M = \undefined and M' = \undefined and w = x u + s -1 1 and w' = y u + s' -1 1 and v = x y
implies
# ...
v = M w + M' w' - In many of the communication examples being considered, it is useful to be able to construct a matrix whose corresponding linear
transformation has a specific non-trivial image, and a specific non-trivial kernel (i.e., the span of a particular vector or set
of vectors). Suppose we know that a vector [x;y] in R2 is a linear combination of two linearly independent vectors:
x y = s ⋅ a c + r ⋅ b d We do not know s and r, but we do know all of the following:
x y , a c , b d One way to remove the [b;d] term from [x;y] is to first set up a matrix equation and solve for s and r:
a b c d ⋅ s r = x y However, suppose we instead want to find a linear transformation f such that for any [x;y] as defined above, we have:
f ( x y ) = s ⋅ a c In fact, given the information we have, we can construct exactly such a linear transformation:
f ( v ) = ( a b c d ⋅ 1 0 0 0 ⋅ a b c d -1) ⋅ v Complete the argument below showing that this linear transformation indeed has this property.
∀ a,b,c,d,x,y,s,r ∈ R,
( a c ) and ( b d ) are linearly independent and
s ⋅ a c + r ⋅ b d = x y
implies
# ...
s ⋅ a c = ( a b c d ⋅ 1 0 0 0 ⋅ a b c d ^(-1)) ⋅ x y
-
Let polynomials in F = {f | f(t) = a t2 + b t + c } represent a space of possible radio signals.
To send a vector v ∈ R3 to Bob, Alice sets her device to generate the signal corresponding to the polynomial in F whose coefficients
are represented by v. Bob then has his receiver sample the radio signals in his environment at three time points to retrieve the message.
-
Suppose Bob samples the signals at t ∈ {1,2,3} and obtains the vectors P defined below. What vector in R3 did Alice send? Use
techniques you have learned in this course to retrieve the vector.
P := { 1 1 , 2 -3 , 3 -11 }
# ...
v := \undefined -
Suppose the environment contains noise from other communication devices; the possible signals in this noise are always from the span
of the following polynomials:
Alice and Bob agree that Alice will only try to communicate to Bob one scalar r ∈ R at a time. They agree on a vector u ahead of time. Any time Alice wants to send some r ∈ R to Bob, she will have her device generate the signal corresponding to the polynomial represented by r ⋅ u. If the vectors P below represent the samples collected by Bob, what scalar was Alice sending to Bob?g(t) = 2 t - 2 h(t) = t2 + 3 t P := { 1 3 , 2 9 , 3 13 }
# ...
s := \undefined -
Suppose there is no noise in the environment. Alice, Bob, and Carol want to send individual scalars to one another at the same time:
all three would be sending a signal simultaneously, and all three would be listening at the same time:
- Alice's device would generate a signal corresponding to a scalar multiple of f(x) = 2 x + 1;
- Bob's device would generate a signal corresponding to a scalar multiple of g(x) = -x2 + 1;
- Carol's device would generate a signal corresponding to a scalar multiple of h(x) = x2 - 3 x.
Suppose you sample the radio signals at a given moment and obtain the vectors P below. Determine which scalars Alice, Bob, and Carol are each transmitting. Your answer can be in the form of a vector.
P := { 0 5 , 1 7 , 2 7 }
# ...
v := \undefined
-
Suppose Bob samples the signals at t ∈ {1,2,3} and obtains the vectors P defined below. What vector in R3 did Alice send? Use
techniques you have learned in this course to retrieve the vector.
Modelling Systems of Populations: Applications of Linear Transformations and Eigenvalues
We introduce a few concepts.
Definition: Given a linear transformation f ∈ Rn → Rn, v ∈ Rn is a fixed point of f if:
f(v) = vExample: Consider the following linear transformation:
f(v) = 2 1 1 2 ⋅ v Then the following vector v is a fixed point of f:
v = -1 1 f( -1 1 ) = 2 1 1 2 ⋅ -1 1 = -1 1 Fact: If v is a fixed point of f and v ∈ ker f, then v = 0.
Fact: For any linear transformation f, 0 is a fixed point of f (see the definition of a linear transformation).
Fact: If v is a fixed point of f and v ≠ 0, then f has an infinite number of fixed points. This is because for any s ∈ R and any fixed point v, we have that:
f(v) = v f(s ⋅ v) = s ⋅ f(v) = s ⋅ v Fact: For any linear transformation f where f(v) = T ⋅ v, let S be the set of fixed points of f:
S = {v | f(v) = v }Then S is a vector space. There are several ways to show this. Let v be any fixed point of f. Then we have:
f(v) = v T ⋅ v = v (T ⋅ v) - v = 0 (T ⋅ v) - I ⋅ v = 0 (T - I) ⋅ v = 0 Thus, the fixed points of f represented by T are exactly the elements of ker h where h(v) = (T - I) ⋅ v, so S = ker h. Alternatively, we could show that S contains 0, S is closed under scalar addition, and S is closed under scalar multiplication.
We can generalize the notion of a fixed point by observing that a fixed point is just a vector on which the linear transformation acts as a scalar multiplier (in the case of a fixed point, the multiplier is 1). If v is a fixed point of f, then we have that:
f(v) = 1 ⋅ vWhat if we created another notion that was not restricted to 1?
Definition: Given a linear transformation f ∈ Rn → Rn, v ∈ Rn is an eigenvector of f with eigenvalue λ if:
f(v) = λ ⋅ vFact: For any linear transformation f, if v is a fixed point of f, then it is an eigenvector of f with eigenvalue 1.
Definition: The set of eigenvectors of a linear transformation f is its eigenspace.
Fact: Given a linear transformation f ∈ Rn → Rn represented by T ∈ Rn×n and an eigenvector v, consider the following:
f(v) = λ v T ⋅ v = λ v (T ⋅ v) - λ v = 0 (T ⋅ v) - λ I ⋅ v = 0 (T - λ I) ⋅ v = 0 The above equation has only zero solutions if (T - λ I) is invertible:
(T - λ I) ⋅ v = 0 (T - λ I) -1 ⋅ (T - λ I) ⋅ v = (T - λ I) -1 ⋅ 0 v = (T - λ I) -1 ⋅ 0 v = 0 Thus, nonzero eigenvectors v only if (T - λ I) is not invertible. However, this means that det (T - λ I) = 0. Thus, if it is the case that det (T - λ I) = 0, then there must exist at least one λ that solves this equation. In fact, the eigenvalues of T are exactly the solutions to the equation:
det (T - λ I) = 0 Example: Suppose that we are modelling a system with two dimensions that are each modelled using R:
- population in the city;
- population in the suburbs.
The following matrix (call it T) represents the movement of the two populations between the two locations (with entries in percentages) over one year:
from city from suburbs to city 0.95 stay in the city 0.03 move from suburbs to city to suburbs 0.05 move from city to suburbs 0.97 stay in the suburbs For example, suppose the population in 1999 is represented by v below. Then the population in 2000 is represented by T ⋅ v:
T ⋅ v = 0.95 0.03 0.05 0.97 ⋅ 600,000 400,000 = 582,000 418,000 Let f(v) = T ⋅ v be the linear transformation represented by T.
- What does a fixed point of f represent?
A fixed point of f represents a stable population distribution that will not change from one year to the next. For example:
0.95 0.03 0.05 0.97 ⋅ 375,000 625,000 = 375,000 625,000 Notice that any scalar multiple of this vector, including a vector that is normalized so that the two components add up to 1, is also a fixed point of f:
0.95 0.03 0.05 0.97 ⋅ 375,000 625,000 = 0.375 0.625 Thus, for this transformation, for any distribution of the population in which 37.5% live in the city, the distribution is stable.
- What does an eigenvector of f represent?
An eigenvector of f represents a population distribution that may grow or shrink, but whose relative distribution between the city and the suburbs remains the same from one year to the next.
-
Does f have any nonzero eigenvectors other than the fixed points?
No, because the sum of the components of any vector in im f is always the same as the sum of the components of the input vector that produced that image.
0.95 0.03 0.05 0.97 ⋅ x y = 0.95 x + 0.03 y 0.05 x + 0.97 y x + y = (0.95 x + 0.05 x) + (0.03 y + 0.97 y) = (0.95 x + 0.03 y) + (0.05 x + 0.97 y) This is because the sums of the components of the column vectors of T are 1. This makes T a stochastic matrix, and it makes the fixed points the steady-state or equilibrium vectors of T.
-
Find the vector space of fixed points of f.
Note that either the fixed points of f are {0}, or there are infinitely many. Thus, if we can find a matrix equation whose solutions are the fixed points, we will obtain either a system whose only solution is 0, or an underdetermined system. We know that for our particular f and T, the space of fixed points is ker h where:
h(v) = ( 0.95 0.03 0.05 0.97 - 1 0 0 1 ) ⋅ v = -0.05 0.03 0.05 -0.03 ⋅ v We know that ker h consists of the vectors in the orthogonal complement of the row vectors of (T - I). Recall that if g(v) = (T - I)⊤, then ker h = (im g)⊥. Also, since the row vectors of (T - I) are linearly dependent (the top row multiplied by -1 yields the bottom row and vice versa), we know that dim ker h = 1. Thus,
ker h = {v | v ⋅ -0.05 0.03 = 0} = span { 0.03 0.05 } = span { 3 5 } -
Suppose we want to find a closed formula for the population k years after the initial state v (i.e., after applying T to an initial
vector v eight times, or Tk ⋅ v) where we have:
v = 0.6 0.4 The formula should be in terms of k and should not require matrix multiplication. In other words, we should be able to obtain closed formulas for the city population and the suburb population in terms of k.
We can approach this problem by finding the eigenvectors of f, which span its eigenspace. Then, we can express the result of Tk ⋅ v as a linear combination of eigenvectors.det ( 0.95 0.03 0.05 0.97 - λ ⋅ 1 0 0 1 ) = 0 det 0.95 - λ 0.03 0.05 0.97 - λ = 0 (0.95 - λ) ⋅ (0.97 - λ) - (0.03 ⋅ 0.05) = 0 λ2 - 1.92 λ + 0.9215 - 0.0015 = 0 λ2 - 1.92 λ + 0.92 = 0 λ = (1.92 ± √(1.922 - 4(0.92)))/2 λ = 1.92/2 ± 0.08/2 λ = 0.96 ± 0.04 λ = 1 or 0.92 We already know the eigenvector for eigenvalue 1 (it is the fixed point). To find the eigenvector for the other eigenvalue, we solve:
0.95 0.03 0.05 0.97 ⋅ x y = 0.92 ⋅ x y 0.95 x + 0.03 y = 0.92 x 0.05 x + 0.97 y = 0.92 y 0.03 x + 0.03 y = 0 0.05 x + 0.05 y = 0 x = 1 y = -1 Thus, our eigenvectors are:
e1 = 3 5 e2 = 1 -1 Notice that we had a space of solutions because the system was underdetermined; we chose a particular eigenvector. Finally, notice that:
Tk ⋅ (a ⋅ e1 + b ⋅ e2) = (Tk ⋅ a ⋅ e1) + (Tk ⋅ b ⋅ e2) = a ⋅ (Tk ⋅ e1) + b ⋅ (Tk ⋅ e2) = a ⋅ e1 + b ⋅ 0.92k ⋅ e2 Thus, if the initial input vector can be rewritten in terms of the two eigenvectors, we can find the closed formula. In fact, it can be because the two eigenvectors are linearly independent:
a ⋅ 3 5 + b ⋅ 1 -1 = x y 3 1 5 -1 ⋅ a b = x y a b = 3 1 5 -1 -1 x y a b = 3 1 5 -1 -1 0.6 0.4 a b = 0.125 0.225 0.125 ⋅ 3 5 + 0.225 ⋅ 1 -1 = 0.6 0.4 The closed formula is:
Tk ⋅ 0.6 0.4 = 0.125 ⋅ 3 5 + 0.225 ⋅ 0.92k ⋅ 1 -1
Eigenspaces have many other applications. In particular, they make it possible to provide "natural" interpretations of general notions of concepts such as differentiation in the context of vector spaces.
Example: Differentiation is a linear transformation from the vector space of differentiable functions (or a subset, e.g., the polynomials):
d dx (a f + b g) = a d dx f + b d dx g As an example, consider the space of polynomials of the form f(x) = a x2 + b x + c. If each polynomial is represented as a vector of its coefficients, the differentiation operator for this vector space of functions can be represented as a matrix:
0 0 0 2 1 0 0 1 0 ⋅ a b c = 0 2 a b Thus, an eigenvector in this vector space is any differentiable function f such that:
d dx f = λ f Notice that the above is a differential equation. If λ = 0, then we have for any constant c ∈ R the solution:
f(x) = c If λ ≠ 0 and we do not restrict ourselves to polynomials but allow all infinitely differentiable functions, then we have the solution:
f(x) = c eλx
Review #3
Comprehensive List of Course Topics
The following is a breakdown of what you should be able to do at this point in the course (and of what you may be tested on in the final exam). Notice that many of the tasks below can be composed (e.g., you could find the image of a linear transformation, and then because it is a vector space, you could determine its dimension). This also means that many problems can be solved in more than one way.
- vectors and matrices
- algebraic properties of scalar, vector, and matrix multiplication and vector and matrix addition
- vector properties and relationships
- norm of a vector
- unit vectors
- linear dependence
- linear independence
- dot product of two vectors
- orthogonal vectors
- matrix properties and relationships
- identity matrix
- elementary matrices
- scalar matrices
- diagonal matrices
- upper and lower triangular matrices
- determinant of a matrix
- inverse of a matrix and invertible matrices
- determine whether a matrix is invertible
- algebraic properties of matrix inverses with respect to matrix addition and multiplication
- transpose of a matrix
- algebraic properties of transposed matrices with respect to matrix addition and multiplication
- row echelon form and reduced row echelon form of a matrix
- matrix rank
- vector spaces
- vector spaces and their properties
- given a set of vectors or other objects, show that it is a vector space
- express a vector space as a span of a finite set of vectors
- given two vector spaces, show one is a subspace of the other
- given two vector spaces, show they are equal
- find the orthogonal complement of a vector space
- find the basis of a vector space
- find an orthonormal basis of a vector space
- find the dimension of a vector space
- particular vector spaces
- subsets of Rn and Rn×m
- the set of polynomials of a given order
- vector spaces and their properties
- linear transformations
- show that a map is a linear transformation
- show a linear transformation is surjective
- show a linear transformation is injective
- show a linear transformation is bijective
- given a linear transformation (and/or its matrix representation)...
- show it is injective
- show it is surjective
- show it is bijective
- find its kernel (a vector space)
- find its image (a vector space)
- find its space of fixed points
- compositions of linear transformations and their properties
- given a kernal and image, find a linear transformation (i.e., the matrix that represents it) with that kernel and image
- compute orthogonal projections...
- onto the span of a single vector in Rn
- onto a subspace of Rn...
- by first computing an orthonormal basis and then using it to find the projection
- by using the formula M (M⊤ ⋅ M) -1 M⊤ when ker f = {0} for f(v) = M ⋅ v
- systems of equations and matrix equations
- solve a linear system of the form LU = v
- find the least-squares approximation of an overdetermined linear system
- applications
- systems of states
- interpret a system of states consisting of dimensioned quantities as a vector space
- interpret relationships in a system of states as a matrix
- interpret system state transitions/transformations as matrices/linear transformations
- interpret partial observations of system states as matrices/linear transformations
- given a partial description of a system state and a matrix of relationships, find the full description of the system state
- curve fitting and data approximation
- find a polynomial that fits a given set of points in R2
- find a least-squares approximate curve that best fits a set of points in R2
- communications (sending messages consisting of vectors)
- decrypt message vectors encrypted using a matrix
- eliminate noise from a message vector
- encode a message vector as a polynomial and use sampling to transmit it
- decode a message vector sent as a polynomial
- filter out noise from a message vector sent as a polynomial
- systems of states
- population distributions over time
- find the fixed point of a transition matrix
Practice Problems
Below is a comprehensive collection of review problems going over all the course material. These problems are an accurate representation of the kinds of problems you may see on an exam.
Problem: Consider the following vector space:
V = span{ 2 1 4 , 0 1 -1 } - Find the orthogonal projection of the following vector onto V:
u = 1 2 0 If the two spanning vectors were orthogonal, one approach would be to project u onto a normalized form of each vector, and to add the results. If the two spanning vectors were orthonormal, it would be sufficient to simply project onto each vector, and add the results. Because the two vectors are neither, we must use the formula A (A⊤ A) -1 A⊤ u for the projection whereA = 2 0 1 1 4 -1 - Find a basis of V⊥.
Note that dim V = 2 (since the two spanning vectors are linearly independent), and we know that:dim V + dim V⊥ = 3
Thus, dim V⊥ = 1, so we need one spanning vector of V⊥ that is orthogonal to both spanning vectors of V. It is sufficient to set up an underdetermined system, solve for two of the variables in terms of the third, and set the third to an arbitrary constant:
2 1 4 ⋅ x y z = 0 0 1 -1 ⋅ x y z = 0 2x + y + 4z = 0 y - z = 0 y = z x = -y/2 - 4z/2 = -z/2 - 4z/2 = -5/2 ⋅ z Setting z = 2, we get:
V⊥ = span { -5 2 2 } - Find any matrix M such that for f(v) = M ⋅ v, ker f = V.
It is sufficient to find a matrix that maps both spanning vectors to 0. One approach is to use the formula for a matrix with a specific kernel and image. From above, we already have a vector that spans V⊥, so such a matrix can be computed using the formula:
-5 2 0 2 1 1 2 4 -1 ⋅ 1 0 0 0 0 0 0 0 0 ⋅ -5 2 0 2 1 1 2 4 -1 -1
Problem: Consider the vector space of polynomials of degree at most 2:
F = { f | f(x) = a x2 + b x + c, a,b,c ∈ R}The map d:F → F represent differentiation. For example:
f(x) = 5 x2 - 2 x + 3 g(x) = 10 x - 2 d(f) = g - Determine whether d:F → F is injective.
It is not injective because we can find two unequal inputs that produce the same output. Consider the following polynomials:
f(x) = 1 g(x) = 2 h(x) = 0 Then we have that:
d(f) = h d(g) = h Thus, the map d is not injective.
- Find ker d.
We are looking for the set of all polynomials in F whose derivative is the polynomial f(x) = 0. We know this is exactly the set of polynomials:{f | f(x) = 0 x2 + 0 x + r, r ∈ R}
- Recall that a polynomial can be represented as a vector. For example, f(x) = 5 x2 - 2 x + 3 can be
represented as:
Show that d is a linear transformation by finding a matrix representation for d.5 -2 3 The matrix is:0 0 0 2 1 0 0 1 0 Notice that:
0 0 0 2 1 0 0 1 0 ⋅ a b c = 0 2 a b - Show that d:F → F is not surjective by using im and dim.
In order for a linear transformation to be surjective, it must be that dim im = dim F. We know that dim F = 3, and we also know that there are only two linearly independent columns in the matrix representing d, so dim (im d) = 2. Thus, dim F ≠ dim (im d), so there must be vectors in the codomain of d that are not in the image of d, so d is not surjective.
Problem: Alice wants to send vectors in R2 to Bob. For any vector v ∈ R2 that she wants to send, she generates a random scalar r ∈ R and sends w to Bob as defined below:
v = x y w = 1 2 -1 0 3 1 0 0 2 x y r - Find a matrix D ∈ R3× 3 that Bob can use to decode Alice's messages.
Alice is sending vectors that are a linear combination of two vectors that carry the two scalars in a message vector v and a noise vector:
1 0 0 x + 2 3 0 y + -1 1 2 z Bob must first cancel out the noise using a matrix in R3 that has the appropriate kernel. Then he must take the result of that and recover the scalars x and y.
To find an appropriate matrix to cancel out the noise, Bob can use the following formula:
C = 1 2 -1 0 3 1 0 0 2 ⋅ 1 0 0 0 1 0 0 0 0 ⋅ 1 2 -1 0 3 1 0 0 2 -1 Once Bob applies C to the vector he receives from Alice, he has:
1 0 0 x + 2 3 0 y + 0 0 0 ⋅ 0 = 1 2 0 0 3 0 0 0 0 x y 0 Notice that we can find a matrix that inverts this operation by replacing the top-left portion of the above encoding matrix with its inverse:
1 2 0 3 -1 = 3 -2 0 1 D = 3 -2 0 0 1 0 0 0 0 3 -2 0 0 1 0 0 0 0 1 2 0 0 3 0 0 0 0 x y 0 = x y 0 Thus, Bob can use the following matrix to decode messages:
D ⋅ C.If Bob receives a message w that is the encoded version of v, he can retrieve it by computing:
D ⋅ C ⋅ w. - Find a matrix D' ∈ R2×3 that Bob can use to retrieve v ∈ R2 given a transmitted w ∈ R3.
Bob simply needs to drop the third component of the result of D ⋅ C ⋅ w. This can be accomplished by computing:
1 0 0 0 1 0 ⋅ D ⋅ C ⋅ w Thus, an appropriate matrix in R2×3 would be:
1 0 0 0 1 0 ⋅ D ⋅ C
Problem: Suppose there are two locations across which a population is distributed. Over the course of each year, the population moves between the two locations according to one of two population distribution transformations depending on how well the economy is doing (A if the economy is doing well, B otherwise):
A = 0.55 0.9 0.45 0.1 B = 0.75 0.3 0.25 0.7 - Find an initial state v ∈ R2 such that if the economy is always doing well,
the population distribution will remain the same.
We need to find a fixed point of f(v) = A ⋅ v. Since dim R2 = 2, we know that there are three possibilities:
- 0 is the only fixed point;
- the space of fixed points has dimension 1, so there are infinitely many fixed points that all fall on a single line;
- all points in R2 are fixed points.
We solve the following system:
0.55 0.9 0.45 0.1 ⋅ x y = x y 0.55 x + 0.9 y = x 0.9 y = 0.45 x 0.45 x + 0.1 y = y 0.45 x = 0.9 y x = 2 y Since one equation can be derived from the other, the above system is underdetermined, but x can be expressed in terms of y. Thus, the space of fixed points is one-dimensional. Setting y = 10, it can be expessed as a span of the following fixed point vector:
20 10 - Suppose that over the course of several years, the economy has both done well and not well.
Has the total population (the sum of the populations in the two locations) changed over this
duration?
Notice that neither A nor B change the total population in the two locations as represented by a state vector in R2. Thus, the total population has not changed.
Appendix
This section contains a short review of concepts used in this course that are found throughout mathematics.
Logical formulas and quantifiers
A mathematical formula is a string of symbols that follow a certain syntax. If it the formula is written using a correct syntax, we can ask whether the formula is true or false.
formula true or false example \true always true
3 = 3
\true\false always false
1 < 2
\falsef1 \and f2 only true if both f1 and f2 are true
1 < 2 and 2 < 3f1 implies f2 true if assuming f1 can let us derive f2
always true if f1 is false (i.e., proof by contradiction)
1 = 2 and 2 = 3 implies 1 = 3∀ x ∈ S, f true if no matter what element we choose in S,
substituting x for that element in f will result
in a true formula
∀ x ∈ {1,2,3}, x > 0
∀ x ∈ {1,2,3}, x > 2∃ x ∈ S, f true if there is at least one element in S such that
substituting x for that element in f will result
in a true formula
∃ x ∈ {1,2,3}, x = 2
∃ x ∈ {1,2,3}, x > 3Set comprehensions
Set comprehension notation is a way to specify how sets can be built or filtered by using formulas.
set comprehension description result example {x | x ∈ {1,2,3,4}} take each element in S and put it in
the set represented by {x | x ∈ S}{1,2,3,4} {x | x ∈ {1,2,3,4}, x > 2} take each element in S and put it in
the result set only if it is greater than 2{3,4}
{ x | x ∈ {1,2,3,4}, x > 2}{x | x ∈ S, f} take each element in S and put it in
the result set only if substituting x in f
with that element results in a true formula
{ x |
x ∈ {1,2,3,4},
∃ y ∈ {3,4}, x = y
}Sets and operators
We often consider sets together with operators over those sets. These operators can have properties related to those sets.
Operators allow us to construct syntactic terms that are then interpreted as referring to elements in a set. When two syntactic terms refer to the same element in a set (i.e., have the same meaning), such as 1+(2+3) and (3+2)+1, we say they are equivalent:
1+(2+3) = (3+2)+1.We have names for several common properties that operators may possess for a given set. In the table below, We define them precisely using logical notation.
property definition S is closed under ⊕ ∀ x,y ∈ S,
x ⊕ y ∈ S⊕ is commutative on S ∀ x,y ∈ S,
x ⊕ y = y ⊕ x⊕ is associative on S ∀ x,y,z ∈ S,
(x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)⊕ has a left identity I in S ∀ x ∈ S,
I ⊕ x = x⊕ has a right identity I in S ∀ x ∈ S,
x ⊕ I = x⊕ has an identity I in S ∀ x ∈ S,
I ⊕ x = x ⊕ I = x⊗ distributes across ⊕ in S ∀ x,y,z ∈ S,
x ⊗ (y ⊕ z) = (x ⊗ y) ⊕ (x ⊗ z)Equality is assumed to be reflexive, symmetric, and transitive.
property definition = is reflexive for S ∀ x ∈ S,
x = x= is symmetric for S ∀ x,y ∈ S,
x = y iff y = x= is transitive for S ∀ x,y,z ∈ S,
x = y and y = z implies x = zRelations, maps, and functions
A relation between two sets X and Y is simply a subset of the collection of all pairs of objects drawn from two sets.
construct definition example graphical example X × Y { (x,y) | x ∈ X, y ∈ Y } {1,2,3} × {4,5,6}
=
{(1,4),(1,5),(1,6),
(2,4),(2,5),(2,6),
(3,4),(3,5),(3,6)}R is a relation between X and Y R ⊂ X × Y {(1,D), (2,B), (2,C)}
is a relation between
{1,2,3,4} and {A,B,C,D}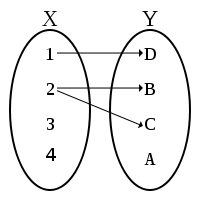
f is a function from X to Y f is a relation between X and Y and
∀ x ∈ X, there is exactly one
y ∈ Y s.t. f relates x to y{ (x,f(x)) | f(x) = x2 } 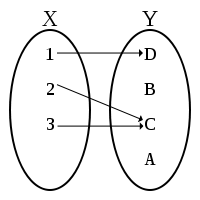
R -1 is the inverse of R { (b,a) | (a,b) ∈ R } f: X → Y is injective 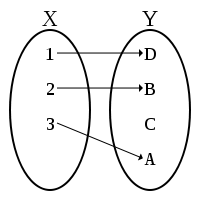
f: X → Y is surjective 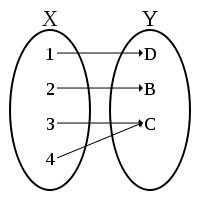
f: X → Y is bijective 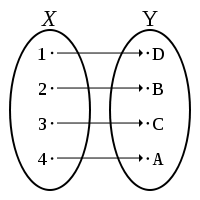
Notice that we may have f such that f is a function, but f -1 is not a function.